InfoC adventi naptár

Teknőcgrafika

A programozásban sokszor egy probléma megoldásának úgy érdemes nekiindulni, hogy kitalálunk egy új nyelvet, amellyel (amelyen) a megoldást könnyebben megfogalmazhatjuk. Gondoljunk bele: ha a kitalált nyelv szavait, kifejezéseit lefordítjuk C nyelvre (pl. C- beli függvényhívásokra), akkor a C nyelv lehetőségeit (ciklusok, változók, függvények stb.) automatikusan kapjuk melléjük kiterjesztésként. Vagyis a kitalált nyelvünknek automatikusan részévé válnak a C nyelv kombinációs és absztrakciós lehetőségei.

Ilyen kitalált nyelv a teknőcgrafika, amely sokak számára Comenius Logo néven lehet ismerős. Képzeljük el, hogy egy teknős sétál a képernyőn. Van nála egy ceruza, amellyel vagy húz vonalat séta közben, vagy nem. A következő utasításokat kaphatja:

• Emelje fel a ceruzát. (A mozdulatai így nem fognak látszani.)
• Tegye le a papírra a ceruzát. (A nyoma így megmarad.)
• Sétáljon előre valamennyit.
• Forduljon el valahány fokkal.

Ezen a nyelven egy négyzet rajzolása így fogalmazható meg:

Ha megírjuk az alap teknőcműveleteket C-ben, akkor annak képességei kiterjesztik a teknőcgrafika képességeit is. A fenti példában az ismétlés lesz a C for() ciklusára cserélhető:

Tedd le a ceruzát.
for (i=0; i<4; ++i) {
   Sétálj előre 5 centit.
   Fordulj balra 90 fokkal.
}

Innentől kezdve pikk-pakk megy minden, használhatunk változókat, ciklusokat, írhatunk függvényeket, amelyek bonyolultabb műveleteket végeznek el és így tovább. Együtt használhatjuk a C nyelv adta lehetőségeket a grafikus nyelvünkkel. A fenti négyzet könnyen általánosítható akárhány oldalú szabályos sokszögre, ha nem 360/4=90 fokot fordulunk, hanem 360/n fokot, ahol n a csúcsok száma. Erre is írhatunk C függvényt:

void sokszög(int csúcsok, double oldalhossz) {
   int i;
   for (i=0; i<csúcsok; ++i) {
      Sétálj előre oldalhossz centit.
      Fordulj balra 360/csúcsok fokot.
   }
}

A rajzolás megvalósításához az SDL függvénykönyvtárat használja a letölthető program. Ez egy viszonylag egyszerű, játékok írásához kifejlesztett függvénykönyvtár. A telepítéséről és használatáról az Érdekességek menü SDL menüpontja alatt már írtunk.

typedef struct Teknoc {
   double x, y;   /* pozicio */
   double szog;   /* szog */
   int rajzol;    /* rajzol-e mozgas kozben */
   Uint32 szin;   /* szin */
} Teknoc;

A teknőc a következő adatokkal rendelkezik, amelyeket egy struktúrában tárolhatunk:

• koordináta a képernyőn,
• irány (merre néz),
• ceruza lent/fent
• és a ceruza színe.

Az egyes alap lépésekhez mind érdemes függvényeket írni, amelyek első paraméterükként átveszik azt a teknőcöt, amellyel dolgoznak. Így ingyen kapjuk azt a lehetőséget is a teknőcgrafikánkat most megalapozó C-ből, hogy több teknőcöt hozzunk létre, amelyek egymástól függetlenül tudnak rajzolni.

A függvények implementálása egyszerű. A legbonyolultabb függvény lent látható, és az előrefelé sétálást valósítja meg. (Ez is csak néhány sorból áll.) Ebben kapunk egy hosszt – ennyit kell a teknőcnek előre mennie. Az elmozdulás irányát az adja meg, hogy éppen merre néz. A képernyőn ennek komponensei az r·cos(szög) és r·sin(szög) képletekkel számolhatóak. A math.h szögfüggvényeinek a szöget radiánban kell megadnunk. A lenti kódrészletben a line() az SDL függvénye, és egy szép, „simított” szakaszt rajzol. Első paraméterével adjuk meg, hogy hova rajzoljon – screen azt jelenti, hogy közvetlenül a képernyőre. A további paraméterei a kezdő- és végpontok, illetve a szín.

void teknoc_elore(Teknoc *t, double r) {
   double const deg2rad=3.14159265358979323846/180.0;
   double ujx=t->x+r*cos(t->szog*deg2rad),
          ujy=t->y-r*sin(t->szog*deg2rad);
   if (t->rajzol)
      aalineColor(screen, t->x, t->y, ujx, ujy, t->szin);
   t->x=ujx;
   t->y=ujy;
}

A letölthető kódban a további megvalósított függvények az alábbiak:

/* inicializal egy teknocot: kepernyo kozepe, jobbra nez, nem rajzol */
   void teknoc_init(Teknoc *t);
/* beallitja a ceruza szinet, rgb: voros, zold, kek komponensek 0..255 */
   void teknoc_szin(Teknoc *t, Uint8 r, Uint8 g, Uint8 b);
/* leteszi a ceruzat */
   void teknoc_rajzol(Teknoc *t);
/* felemeli a ceruzat */
   void teknoc_nemrajzol(Teknoc *t);
/* balra fordul valahany fokkal */
   void teknoc_fordul(Teknoc *t, double dszog);
/* teleportal az adott kepernyokoordinatakra es iranyba */
   void teknoc_teleport(Teknoc *t, double ujx, double ujy, double ujszog);

Fraktálok ismétlődő részekből álló görbék, minták, amelyek dimenziószáma nem egész szám. (Vigyázat: nem ez a pontos, matematikai definíció.) Mit jelent ez? A pontokról tudjuk, hogy nincs kiterjedésük: nulla dimenziósak. Egy görbének hossza van: egy dimenziós. Egy síkidomnak két irányban van kiterjedése, ezért két dimenziós, míg egy testnek három irányba. A fraktáloknál nem ilyen egyszerű a helyzet.

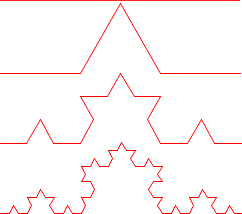
Nézzük meg egy kicsit jobban az ábrát. Ez a következőképpen keletkezik. Először adott egy szakasz (legyen ez egységnyi hosszú). Ezt a szakaszt elharmadoljuk, és a középső harmadot kicseréljük két egyharmad hosszú szakaszra (minta egy egyenlő oldalú háromszög lenne). Az így kapott töröttvonal hossza 4×1/3, azaz 4/3 lesz, ami az eredeti szakasz hosszának 4/3-adszorosa.

Ha ezt a műveletet megismételjük minden 1/3 hosszú szakaszra, a keletkező töröttvonalak hossza 4/3×1/3 lesz, és mivel összesen 4 van belőlük – az összegzet hosszuk 4/3×4/3, tehát (4/3)². Így haladva minden lépésben a hossz az előző 4/3-szorosa lesz, tehát L=(4/3)ⁿ az n-edik lépés után. Ez nem korlátos: n növelésével a végtelenbe tart! Miért érdekes ez annyira? Azért, mert az ábra mérete viszont korlátos. Könnyen rajzolhatunk egy téglalapot, amelybe belefér, tehát az elfoglalt területe korlátos, a töröttvonal hossza mégsem az! Mivel csak egy vonalról van szó, nem mondhatjuk, hogy két dimenziós. Azt sem, hogy egy dimenziós, mivel a hossza bármely két tetszőleges pontja között is végtelen.

Mivel a fenti, teknőcös függvényeket használhatjuk a saját, C-ben megírt rekurzív függvényünkben, így ezek a rajzok könnyen elkészíthetőek. Az előbb leírt görbéhez, Koch görbéjéhez az alábbi rekurzív algoritmus vezet:

• Ha n=0, akkor egy egyenes szakaszt kell rajzolni,
• Ha n>0, akkor pedig a következőket kell tenni:
  • Kirajzolni az n-1-es ábrát,
  • Elfordulni balra 60 fokkal, újabb rajzot készíteni,
  • Jobbra fordulni 120 fokkal, újabb rajz,
  • Balra 60 fok, és újabb rajz.

A fentiek C-ben, vagy éppen teknőcgrafikában, kinek hogy tetszik:

void fraktal(Teknoc *t, int mennyi, double mekkora) {
   if (mennyi==0)
      teknoc_elore(t, mekkora);
   else {
      fraktal(t, mennyi-1, mekkora);
      teknoc_fordul(t, 60);
      fraktal(t, mennyi-1, mekkora);
      teknoc_fordul(t, -120);
      fraktal(t, mennyi-1, mekkora);
      teknoc_fordul(t, 60);
      fraktal(t, mennyi-1, mekkora);
   }
}

Ha egy hatszög oldalait cseréljük ilyen rajzokra, akkor egy hópelyhet kapunk. Kifordítva a rajzokat megkapjuk Koch hópelyhét is. Rengeteg ilyen tulajdonságú görbét lehet találni: David Hilbert térkitöltő görbéje is ilyen. Ezeket mind nagyon könnyű teknőcgrafikával, és az azt most megvalósító C nyelv egyik eszközével – a rekurzióval – megrajzolni.

/* hópelyhet rajzol */
for (i=0; i<6; ++i) {
   fraktal(&t, 2, 10);
   teknoc_fordul(&t, 60);
}

A program letölthető innen: advent8-teknoc.c. A lefordításhoz az SDL című írás ad segítséget (lásd az Érdekességek menüpontot – Windowshoz és Linuxhoz).