3. gyakorlat: C forráskód, vezérlési szerkezetek

A megoldóképlet az alábbi. Arra kell figyelni, hogy ne vonjunk negatív számból négyzetgyököt. A gyökvonás előtt a diszkrimináns vizsgálatával meg kell néznünk, hány valós megoldás lesz.

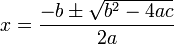
Itt egy nagyobb C kifejezést kapunk, amiben többféle operátor (összeadás, kivonás, szorzás stb.) szerepel. Ezeknek a műveleteknek C-ben ugyanúgy van precedenciája, mint a matematikában. A szorzás pl. magasabb rendű művelet, mint az összeadás. A C nyelv precedencia szabályai összetettebbek; erről majd előadáson lesz szó.

#include <math.h>
#include <stdio.h>

int main()
{
    double a, b, c;
    double diszkr;

    printf("a="); scanf("%lf", &a);
    printf("b="); scanf("%lf", &b);
    printf("c="); scanf("%lf", &c);

    /* a diszkriminans: bnegyzet - 4ac */
    diszkr=b*b-4*a*c;

    /* ha <0, 2 komplex gyok lenne */
    if (diszkr<0) {
        printf("Nincs valos gyok!\n");
    }
    else {
        /* ha pont 0, akkor 1 megoldas van */
        if (diszkr==0) {
            printf("Egy valos gyok: %f\n", -b/(2*a));
        }
        else {
            /* ha ide elerunk, akkor csak pozitiv lehet */
            printf("Ket gyok: %f, %f\n",
                (-b+sqrt(diszkr))/(2*a),
                (-b-sqrt(diszkr))/(2*a));
        }
    }

    return 0;
}

Az if (diszkr==0) vizsgálat elméletben helyes, gyakorlatban azonban nem előnyös ilyet írni. A kerekítési hibák miatt előfordulhat az, hogy 0-hoz olyan közeli szám adódik, amit már 0-ra kerekít a számítógép. Erről később lesz szó előadáson.

Az okos megoldás itt az, ha rájövünk, hogy végülis ezek a számok úgy alakulnak ki, hogy 10-től 99-ig számolunk, és minden szám mellé odaírjuk még egyszer az első számjegyet (pl. 10 mellé az 1-et, 101, vagy 57 mellé az 5-öt, 575). Érdemes ehhez két egymásba ágyazott ciklust írni. Az első számjegy nem lehet 0-s, a második, középső viszont igen, erre figyelni kell.

Megfigyelhetjük azt, hogy mindkét ciklus számlálásos jellegű: a külső 1-től 9-ig megy, a belső 0-tól 9-ig. Az alsó ábra egy nem szabályos, de nagyon szemléletes rajzot tartalmaz. Hasonlítsuk össze a két megoldást áttekinthetőség szempontjából!

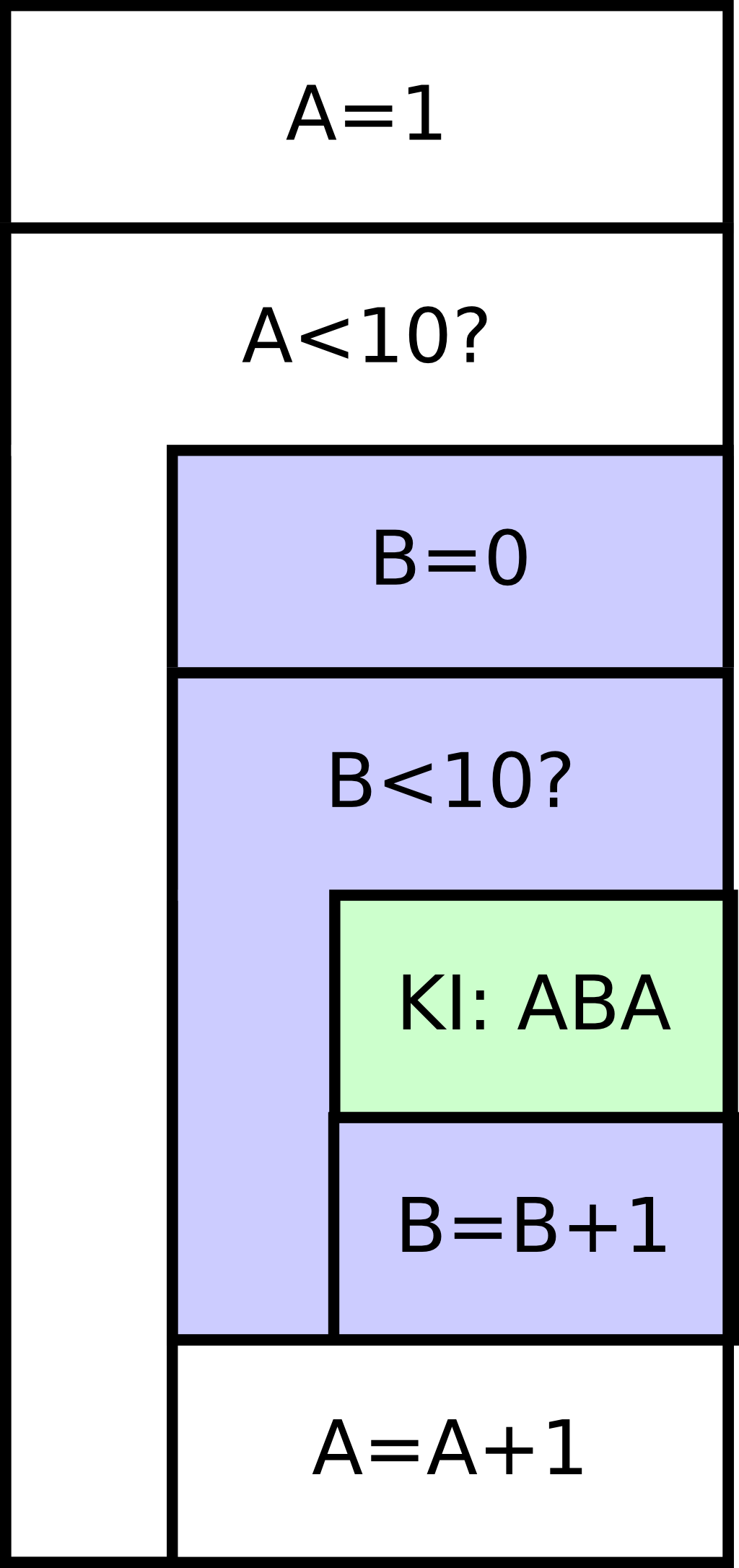
#include <stdio.h>

int main()
{
   int a, b;

   a=1;
   while (a<10) {
      b=0;
      while (b<10) {
         /* aba: tükörszám! */
         printf("%d%d%d ", a, b, a);
         b=b+1;
      }
      a=a+1;
   }

   return 0;
}

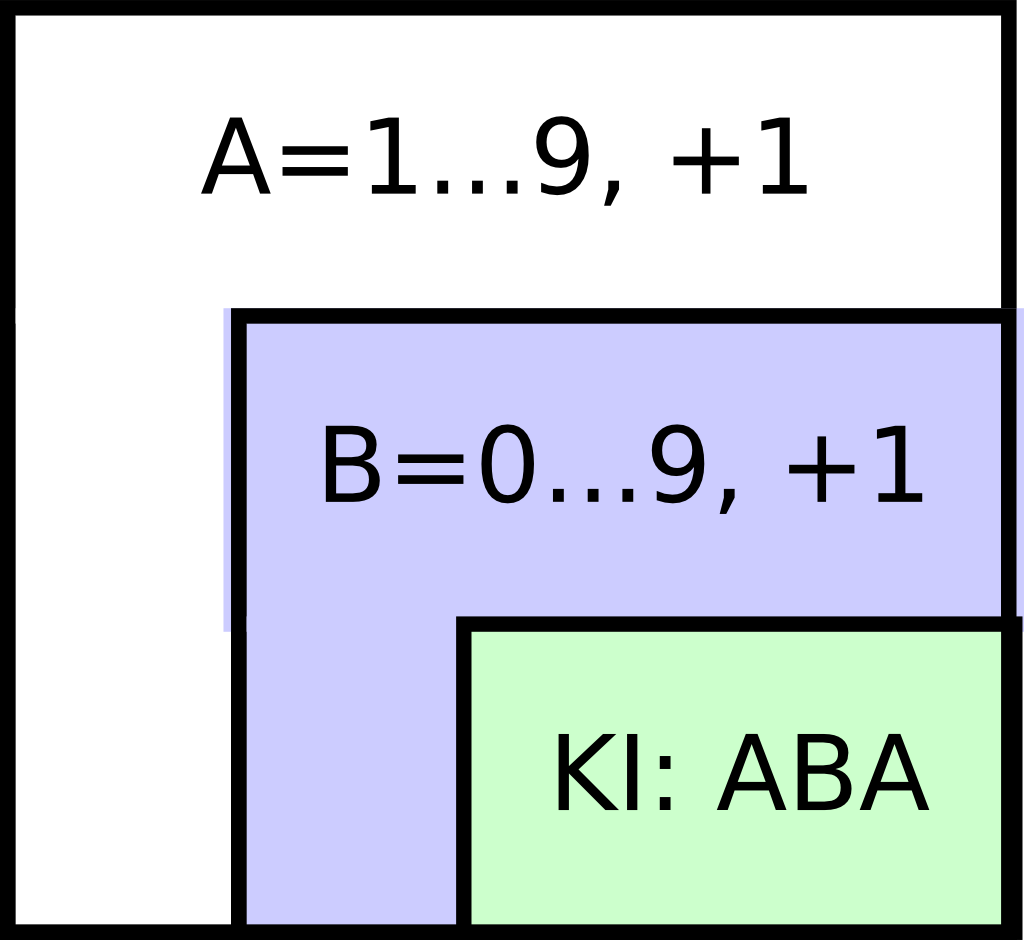
#include <stdio.h>

int main()
{
   int a, b;
   
   for (a=1; a<=9; a=a+1)
      for (b=0; b<=9; b=b+1)
         /* aba: tükörszám! */
         printf("%d%d%d ", a, b, a);    
   
   return 0;
}

A feladat megoldásának kulcsa egy rajz készítése… És annak meghatározása, hogy melyik sorban hány golyó és hány szóköz van. Aki ide eljut, annak nyert ügye van.

#include <stdio.h>

int main()
{
    int magas;
    int sor, x;

    printf("Milyen magas legyen a kupac? ");
    scanf("%d", &magas);

    /* sorok ciklusa */
    for (sor=0; sor<magas; sor=sor+1) {
        /* a sor elejen kell valamennyi szokoz */
        for (x=0; x<magas-sor-1; x=x+1)
            printf(" ");
        /* utana valahany darab o */
        for (x=0; x<sor*2+1; x=x+1)
            printf("o");
        /* sor vege */
        printf("\n");
    }
}

A lenti megoldás mindig egy egész sort ír ki, pl. 150|2. Egy kiírás akkor történik meg, amikor az oszthatóságot már megvizsgáltuk, és a maradék nullának adódott. A 150|2 azt jelenti, hogy a 150-et osztjuk el 2-vel; ezért a konkrét osztás előtt írjuk ki a sort, hogy még az osztás előtti szám látszódjon. Így aztán az utolsó sort, amelyben az 1-es van, külön utasítással kell kiírni.

#include <stdio.h>

int main()
{
   int szam, oszto;
   
   printf("Melyik számot? ");
   scanf("%d", &szam);
   
   oszto=2;
   while (szam>1) {
      if (szam%oszto==0) { /* ha osztható */
         printf("%5d|%d\n", szam, oszto);
         szam=szam/oszto;
      }
      else
         oszto=oszto+1;    /* ha nem */
   }
   printf("%5d\n", 1);
   
   return 0;
}

Esetleg logikusabb lehet az, ha mindig kiírjuk előre a számot, osztani fogunk, és az oszthatóság vizsgálata után már csak az osztót. Ez is helyes megoldás. Ilyenkor az eredeti számot ki kell a ciklus előtt külön. A végén viszont az 1-et nem, mert az a legutolsó osztásnál megjelenik:

#include <stdio.h>

int main()
{
   int szam, oszto;
   
   printf("Melyik számot? ");
   scanf("%d", &szam);
   
   oszto=2;
   printf("%5d|", szam);
   while (szam>1) {
      if (szam%oszto==0) { /* ha osztható */
         printf("%d\n", oszto);
         szam=szam/oszto;
         printf("%5d|", szam);
      }
      else
         oszto=oszto+1;    /* ha nem */
   }
   
   return 0;
}

Érdemes mindkét változat működését végiggondolni, papíron követni vagy nyomkövetővel kipróbálva megvizsgálni!

Rajzoljunk folyamatábrát vagy struktogramot a programhoz! Először írjunk pár példát római számra, és figyeljük meg, milyen sorrendben kell kiírni az egyes értékeket jelző betűket és betűpárokat! Vegyük észre, hogy az XC (90) csak egyszer szerepelhet, míg pl. az X (10) többször is!

#include <stdio.h>

int main()
{
   int x;
   
   printf("Mi a szám? ");
   scanf("%d", &x);
   if (x<1)
      printf("Pozitiv szamot kerek!\n");
   else if (x>99)
      printf("Csak 99-ig tudom.\n");
   else {
      if (x>=90) { printf("XC"); x=x-90; }
      if (x>=50) { printf("L"); x=x-50; }
      if (x>=40) { printf("XL"); x=x-40; }
      while (x>=10) { printf("X"); x=x-10; }
      if (x>=9) { printf("IX"); x=x-9; }
      if (x>=5) { printf("V"); x=x-5; }
      if (x>=4) { printf("IV"); x=x-4; }
      while (x>=1) { printf("I"); x=x-1; }
      printf("\n");
   }
   
   return 0;
}

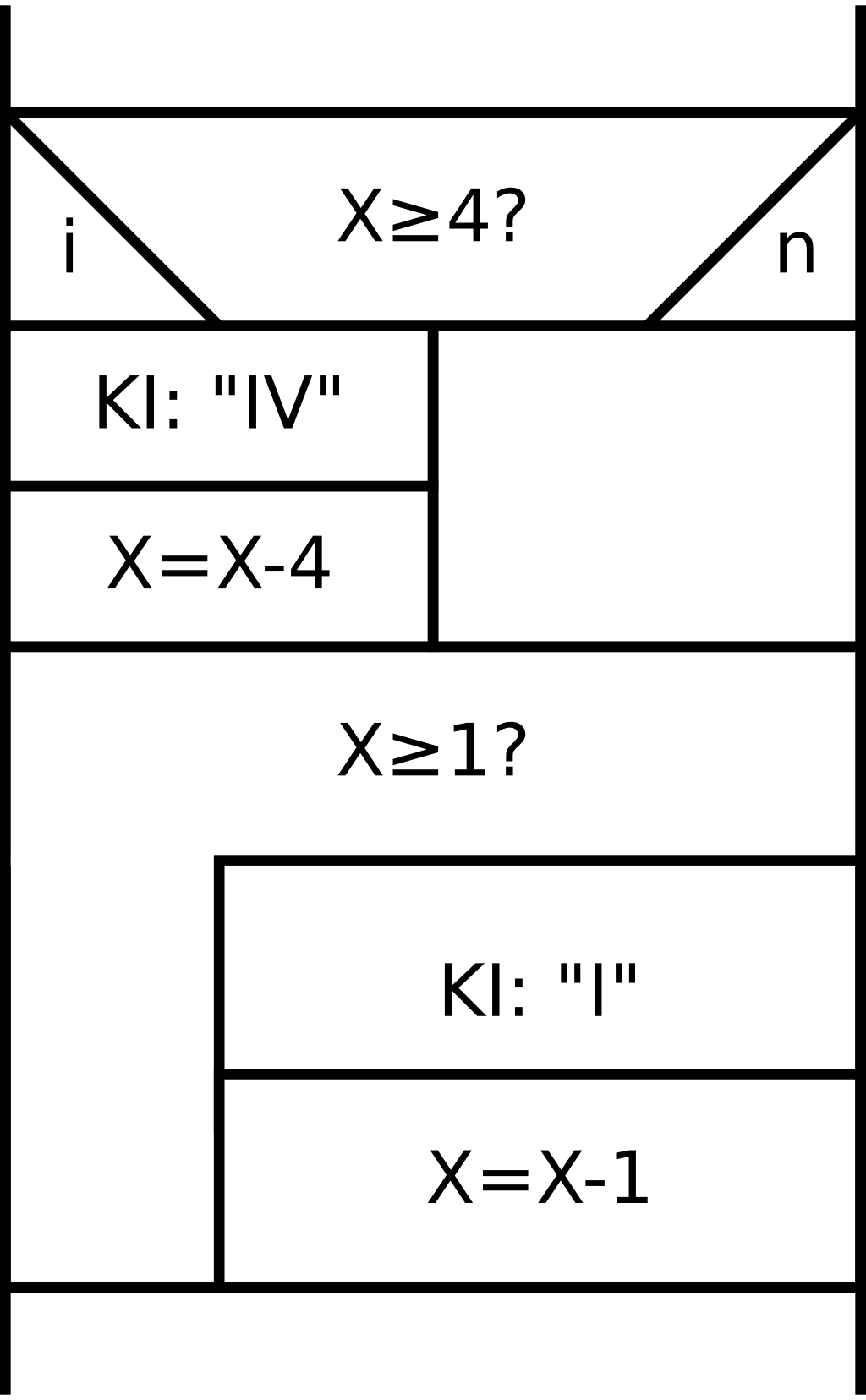
Lehetne máshogy is? Mi történne, ha mindenhol ciklust használnánk? Láthatóan mindegyik számjegynél ugyanazt kell csinálni (kiírni és csökkenteni), ezért aztán a program egy nagy sorminta lett. Egy későbbi gyakorlaton majd javítunk ezen, most egyelőre még hiányzik hozzá a megfelelő C nyelvi eszköz.