13. gyakorlat: fák

typedef struct Szo {
    char szo[30+1];
    int elofordulas;
    
    struct Szo *bal, *jobb;    /* bal es jobb oldali leszarmazottak */
} Szo;

typedef struct Nev {
    char *nev;                 /* tetszőlegesen hosszú név - din. tömb */
    char szam[21];             /* max. 20 karakteres telefonszám */
    struct Nev *bal, *jobb;
} Nev;

typedef struct Morze {
    char betu;
    
    struct Morze *ti, *ta;     /* a kovetkezo jel ti vagy ta lehet */
} Morze;

Itt használhatjuk az strncmp()-t, amely a két sztringet csak valahányadik karakterig hasonlítja össze. A „Nagy” vezetéknevűek név sztringje úgy kezdődik, hogy „Nagy ”, vagyis tuti egy szóköz van a végén (ez pl. a „Nagyító” névnél nem igaz).

A rendezettség lehetővé tenné, hogy szisztematikusan találjuk meg ezeket; itt ezzel nem foglalkozunk, hanem az egész fát bejárjuk.

void nagy_kiir(Nev *gy)
{
    if (gy==NULL) return;

    nagy_kiir(gy->bal);
    /* 5 = strlen("Nagy ") */
    if (strncmp("Nagy ", gy->nev, 5)==0)
        printf("%s %s\n", gy->nev, gy->szam);
    nagy_kiir(gy->jobb);
}

Egy fában annyit találunk a megadott keresett elemből, ahány olyan van a bal oldali, plusz a középső, plusz a jobb oldali részfájában; plusz a csomópont saját tartalma alapján 0 vagy 1. Ezt a C kódban is egy sorba írva látható; a legutolsó sorban a kérdőjel-kettőspontos kifejezés kiértékelve 1-et vagy 0-t ad eredményül, ha az adott elem kisebb n-nél, illetve nem.

A háromágú fa feldolgozása semmiben nem tér el a bináris fáétól – ezt is rekurzívan kell csinálni.

typedef struct TriFa {
    int a;
    struct TriFa *bal, *kozep, *jobb;
} TriFa;

int kisebb(TriFa *p, int n)
{
    if (p==NULL)
        return 0;
    return kisebb(p->jobb, n)
           +kisebb(p->kozep, n)
           +kisebb(p->bal, n)
           +(p->a<n?1:0);
}

Érdemes abból a meghatározásból kiindulni, hogy a gyökértől legmesszebbi levél távolságát kell meghatározni:

1. Üres fa magassága 0.
2. Vegyük a bal és a jobb részfa magasságát.
3. Válasszuk ki a nagyobbat.
4. Adjunk hozzá egyet (aktuális elem távolsága).

typedef struct BinFa {
    int adat;
    
    struct BinFa *bal, *jobb;
} BinFa;

int magassag(BinFa *gyoker)
{
   int bal, jobb, max;

   if (gyoker==NULL) return 0;      /* 1 */

   bal  = magassag(gyoker->bal);    /* 2 */
   jobb = magassag(gyoker->jobb);
   /* melyik magasabb? */
   max  = bal>jobb ? bal : jobb;    /* 3 */

   return max + 1;                  /* 4 */
}

Az összehasonlítás a következő módon képzelhető el. A függvény ebben az esetben két fát kap. Ha mind a két fa üres (NULL), akkor igazat kell válaszoljon; két üres fa ugyanis egyforma. Ha az egyik fa üres, a másik meg nem, akkor nem egyformák (legyen bármi is a másikban, ha az első teljesen üres). Ezekkel a NULL pointeres eseteket lerendeztük. Ha egyik fa sem üres, akkor össze kell hasonlítani őket: akkor egyformák, ha a gyökérelemeik egyformák, és a bal részfáik egyformák, és a jobb részfáik egyformák.

Buktató: hogy két fa inorder bejárással ugyanazt a listát adja, nem biztosan jelenti azt, hogy a két fa egyforma! Egy „5” gyökerű fa, aminek a balra leszármazottja „7”, és annak a balra leszármazottja „9”, a 9-7-5 számsort adja inorder bejárva; a „7” gyökerű fa, amelyiknek a bal leszármazottja „9”, a jobb pedig „5”, úgyszint. Pedig az egyik ilyen / alakú, a másik meg ilyen /\.

int egyforma_e(Fa *egyik, Fa *masik)
{
   if (egyik==NULL && masik==NULL)  /* ket ures fa egyforma */
      return 1;
   if (egyik!=NULL && masik==NULL)  /* ures vs. nem ures -> nem egyforma */
      return 0;
   if (egyik==NULL && masik!=NULL)  /* detto */
      return 0;

   return egyik->szam==masik->szam              /* egyforma szam a gyokerben */
       && egyforma_e(egyik->bal, masik->bal)    /* es egyformak a bal reszfak */
       && egyforma_e(egyik->jobb, masik->jobb); /* es a jobb reszfak */
}

Hogy a két fa egymásnak tükörképe-e, azt ugyanígy lehet ellenőrizni, csak legalul a feltételnél a bal részfát a jobbal kell hasonlítani, és fordítva.

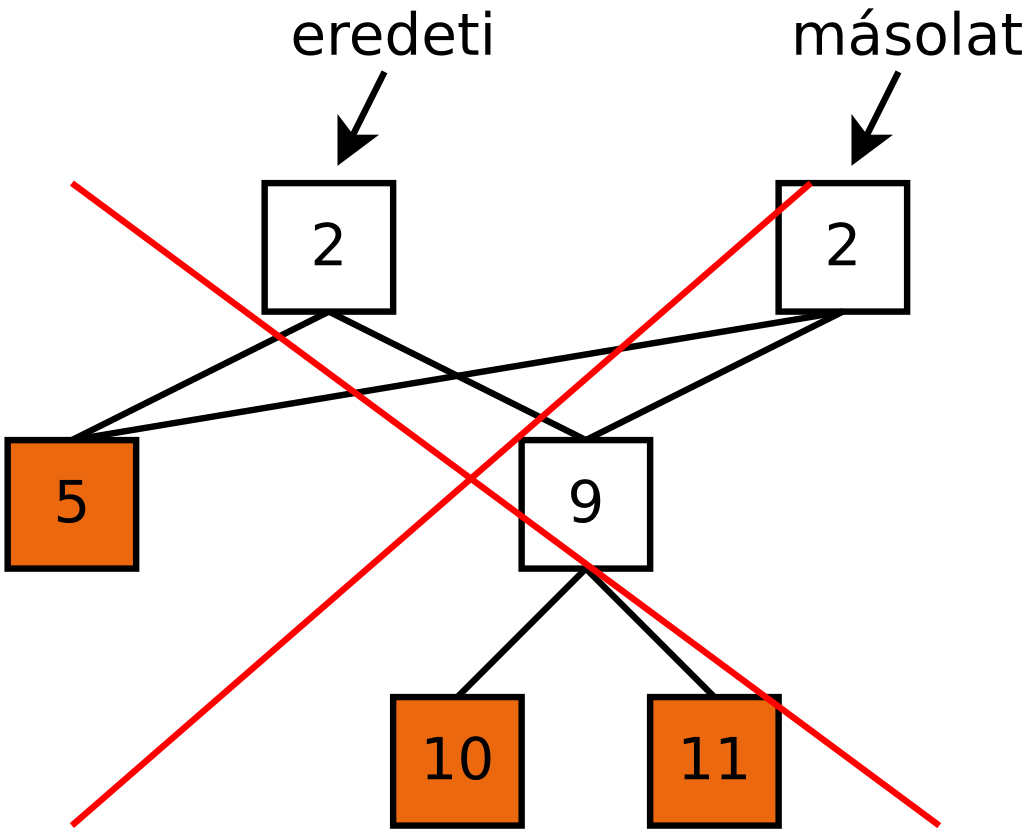
A bináris fa lemásolása nem csak abból áll, hogy egy új pointert ráállítunk a régi fa gyökerére, és azon keresztül ugyanazt látjuk. A másolat egy, az eredetitől teljesen független fa kell legyen, függetlenül módosítható, akár törölhető. Emiatt nem elég az, hogy Fa *masolat=eredeti, és az sem, hogy a gyökér csomópontot lemásoljuk, a pointereivel együtt. Így keletkezne az ábrán látható állapot, amely hibás!

Fa *masolat=(Fa *) malloc(sizeof(Fa));
masolat->adat=eredeti->adat;   ← idáig még akár jó is lehetne
masolat->bal=eredeti->bal;     ← EZ HIBÁS! 
masolat->jobb=eredeti->jobb;   ← EZ IS HIBÁS!

A fa másolása rekurzív: egy másolat csomóponthoz tartozó bal és jobb oldali részfa az eredeti csomópont bal és jobb oldali részfáinak másolata.

Fa *masol(Fa *gy)
{
    Fa *m;

    if (gy==NULL) return NULL;    /* ures fa masolata ures fa */

    m=(Fa *) malloc(sizeof(Fa));  /* uj csomopont es adat */
    m->adat=gy->adat;

    m->bal=masol(gy->bal);        /* reszfak */
    m->jobb=masol(gy->jobb);
    
    return m;
}

Tükrözve lemásolni ugyanígy kell. Csak olyankor a bal részfába kerül a jobb oldalinak a másolata, a jobb oldaliba pedig a bal másolata – persze az egyes másolatok is tükrözve kell legyenek, így ahhoz ugyanúgy csak egy függvény kell, amely a fentitől csak a részfák másolásánál különbözik:

m->bal=tukormasol(gy->jobb);      /* reszfak keresztbe */
m->jobb=tukormasol(gy->bal);

A fát másoló, tükrözve másoló és összehasonlító programok teljes forráskódja letölthető innen: famasol.c