1 Egyszerű ciklus – számok kiírása
Gondolok egy számra, legyen ez 1.
Ismétlés, amíg a szám ≤ 20
Leírom a számot.
Új sort kezdek.
Növelem a számot 1-gyel.
Ismétlés eddig
Az ábrán egy program pszeudokódja látható, amely kiírja a számokat 1-től 20-ig.
Írd meg ezt a programot C-ben while() ciklussal! Figyeld meg:
ahogy gépeled be a while() utáni { kapcsos zárójelet,
az enter billentyű hatására a gép egyből néhány szóközzel beljebb kezdi a sorokat.
A bezáró } kapcsos után pedig újra kintebb. Így áttekinthetőbb
lesz a programod. Használd ezt ki!
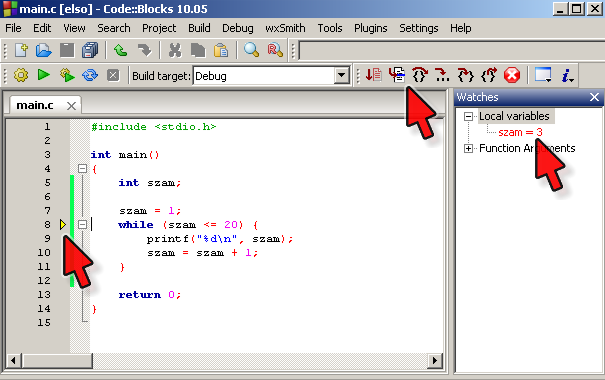
Ha elkészült, futtasd le! Próbáld ki a nyomkövető használatával is! Figyeld meg, hogy a ciklusfeltétel azt mondja meg, hogy meddig ismételjük a műveleteket – amíg a feltétel igaz, addig újból és újból végrehajtja a ciklusmagban lévő utasításokat. Amikor hamissá válik, a ciklusmag utáni utasítással folytatja a végrehajtást.
Figyeld a „Watches” ablakban a ciklusváltozó értékét! Mennyi az
értéke a program futásának vége előtt közvetlenül?
Írd át a while() ciklust for() ciklusra! Végezd el így is a
nyomkövetést!
Emlékeztető: a Code::Blocksban a nyomkövetést legegyszerűbben úgy tudod elindítani, ha arra a sorra állsz a kurzorral, ahol először meg szeretnéd a programot állítani, és megnyomod az F4-et (Debug/Run to cursor). Innentől a program az F7-ttel léptethető soronként (Debug/Next line). A „Debug/Debug windows/Watches” menüponttal hívhatod elő az ablakot, amelyben a változók (Local variables) értékét tudod figyelni.
Számok négyzete. Alakítsd át úgy is a programot, hogy minden szám mellé írja oda annak
négyzetét is. Ezt meg lehet oldani egyetlen printf()
utasítással is!
Páros számok. Alakítsd át úgy a programot, hogy csak a páros számokat írja ki 1 és 20 között! Kell-e paritást (páros/páratlan) vizsgálni ehhez a feladathoz?
Szám beolvasása. Alakítsd át az előző programot úgy, hogy ne 1 és 20 között írja ki a számokat, hanem a felhasználó által megadott határok között! A program indítása után ne csak villogjon a kurzor egy üres ablakban, hanem írja is ki a program, hogy épp mit kérdez, azaz milyen bemenetre vár!
Megoldás
#include <stdio.h>
int main()
{
int mettol, meddig, i;
/* Beolvasás */
printf("Mettol? ");
scanf("%d", &mettol);
printf("Meddig? ");
scanf("%d", &meddig);
/* Az "ettől-eddig-így" ciklusok szebbek,
* áttekinthetőbbek a for (...) változatban */
for (i=mettol; i<=meddig; i=i+1)
printf("%d\n",i); /* Szám kiírása */
return 0;
}
Fordított intervallum. Próbáld ki, mi történik akkor, ha az előbbi programnak fordítva adja meg a felhasználó az intervallum határait (pl. 1–20 helyett 20–1). Nézd meg nyomkövetővel, mi történik! Egészítsd ki úgy a programot, hogy ilyenkor is helyesen működjön!
Megoldás
A releváns programrészlet:
/* Beolvasás */
printf("Mettol? ");
scanf("%d", &hatar1);
printf("Meddig? ");
scanf("%d", &hatar2);
/* Melyik nagyobb? */
if (hatar1<hatar2) {
mettol=hatar1;
meddig=hatar2;
} else {
meddig=hatar1;
mettol=hatar2;
}
2 Számok szorzata
Legyen a szorzat 1.
Legyen n értéke 10.
Ismétlés, amíg n≥2
A szorzat legyen szorzat × n.
Csökkentem n-et eggyel.
Ismétlés eddig
Kiírom a szorzatot.
Módosítsd a programodat úgy, hogy az első 10 szám (1…10) szorzatát, vagyis a 10 faktoriálisát számolja ki! Tegyél a ciklus belsejébe egy olyan programsort is, amely kiírja a ciklusváltozó értékét, és a szorzatot tároló változó értékét is!
Mi történik akkor, ha túl nagy szám faktoriálisát próbálod kiszámítani? Beszéljétek meg a laborvezetővel a tapasztaltakat!
Megoldás
#include <stdio.h>
int main() {
int szorzat;
int n;
szorzat=1;
n=10;
while (n>=2) {
printf("szorzat: %d, n: %d\n", szorzat, n);
szorzat = szorzat*n;
n = n-1;
}
printf("%d", szorzat);
return 0;
}
3 Adott hosszúságú vonal
Írj egy programot, amely kér a felhasználótól egy
számot, és kirajzol egy akkora, + és − jelekből álló szakaszt. Pl.
ha a szám 4, akkor a képernyőn a lenti ábra jelenjen meg,
vagyis a belsejében 4 db − legyen:
Milyen hosszu legyen a vonal? 4 +----+
Írd meg a program pszeudokódját papíron, utána pedig gépen a C forráskódot!
Tipp: ehhez a programhoz nem kell
if()elágazás. Ha olyan változatot írtál, amiben van, akkor próbáld meg anélkül is. Kérd a laborvezető segítségét!
Megoldás
#include <stdio.h>
int main(){
int hossz; /* Vonal hossza */
int i; /* Ciklusváltozó */
printf("Milyen hosszu legyen a vonal? ");
scanf("%d", &hossz); /* Hossz beolvasása */
printf("+"); /* A vonal elejére kell egy + jel */
for (i=0; i<hossz; i=i+1) /* Ciklus, ami kiír adott - jelet */
printf("-");
printf("+"); /* A vonal végére is kell egy + jel */
return 0;
}
4 A Leibniz-féle sor
Leibniz a lenti összegképletet vezette le a π becslésére. Minél több tag szerepel az összegben, annál pontosabb az eredmény. Feladat: írj egy programot úgy, hogy ennek alapján számolja ki a π közelítő értékét!
π 1 1 1 ─ = 1 - ─ + ─ - ─ + … 4 3 5 7
A feladat több buktatót is tartalmaz. Ha nem helyes a program által kiírt eredmény, használj nyomkövetést, figyeld a változók értékét!
Tipp: figyeld meg, hogy az összeadás és a kivonás váltakoznak. Érdemes kettesével, páronként haladni az összegzésben, mert akkor a páros/páratlan vizsgálat kimaradhat a programból.
Fontos: ehhez át kell térned a programban valós típusú változók használatára, hiszen az eredmény biztosan nem egész szám. Tudni kell, hogy ha a C nyelvben elosztasz két egész számot, akkor az eredmény is egész (lefelé kerekítve). Vagyis
1/3értéke C-ben0. Viszont1.0/3értéke0.333333lesz. Erről később részletesen lesz szó előadáson is.
Megoldás
#include <stdio.h>
int main() {
double pi; /* Változó a az eredmény tárolásához */
int i; /* Ciklusváltozó */
/* Ciklus ami páronként halad, azaz egy */
/* lépésben hozzáad és ki is von egy számot */
pi=0;
i=1;
while (i<100000) {
pi = pi + 1.0/i; /* Hozzáadjuk a píhez az aktuális szám reciprokát */
i=i+2; /* Kettővel megnöveljük az aktuális számot */
pi = pi - 1.0/i; /* Levonjuk a szám reciprokát */
i=i+2; /* Kettővel megnöveljük a számot */
}
pi = pi*4; /* A ciklus a pi/4-et közelítette, ezért 4-el szorozni kell */
printf("%f", pi); /* Eredmény kiírása */
return 0;
}
5 Ferde hajítás II.
Emlékezz vissza az előző heti „ferde hajítás” programra.
Ebben t=0 időpillanatban, v0 sebességgel,
alfa szöggel kilövünk egy ágyúgolyót. Írd meg most úgy a programot, hogy t=0,0; 0,1; 0,2; … s
időpontokban (tized másodpercenként) írja ki az ágyúgolyó helyét; egészen addig, amíg
be nem csapódik az a földbe (y≤0)!

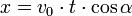
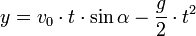
Megoldás
#include <stdio.h>
#include <math.h>
int main()
{
double t, x, y;
double v0, alfa, alfa_rad;
double g = 9.81;
printf("Ferde hajitas\n");
printf("Add meg a kiloves sebesseget!\n");
scanf("%lf", &v0);
printf("Es a kiloves szoget!\n");
scanf("%lf", &alfa);
/* radianban */
alfa_rad = alfa*3.1415926535/180;
t = 0;
x = 0;
y = 0;
while (y>=0) {
printf("t=%8.4f x=%8.4f y=%8.4f\n", t, x, y);
t = t+0.1;
x = v0*t*cos(alfa_rad);
y = v0*t*sin(alfa_rad) - g/2*t*t;
}
printf("t=%.4f s-ra mar biztosan becsapodott.\n", t);
return 0;
}
A fenti megoldás betartja a ciklusokkal kapcsolatos, előadáson
bemutatott játékszabályt. Nevezetesen azt, hogy a ciklustörzs
elején szerepel az aktuális elem feldolgozása (jelen esetben
ez a kiírást jelenti), és a végén a következő elemre lépést
(most ez az idő növelése, és értelemszerűen a koordináták
újraszámolása). Ennek az az előnye, hogy egy már ellenőrzött
y értékkel megyünk be a ciklusba, amelyet külön
feltétel nélkül ki is lehet írni!
Mivel így a ciklus feltétele függ az y koordinátától
(ez amúgy sem lehet másképp, mert a becsapódás időpontját keressük),
az első iteráció előtt már ki kell számolnunk x-et
és y-t. Odamásolhatnánk a ciklus elejére a ferde
hajítás képleteit, de t=0 miatt azok x=0-ra
és y=0-ra egyszerűsödnek.
6 További feladatok
- Írj programot, amely a képernyőre írja a 4, 5 és 6 számjegyekből képezhető összes négyjegyű számot!
- Euler feladata: egy gazda sertést, kecskét és juhot vásárolt, összesen 100 állatot, pontosan 600 aranyért. A sertés darabja 21 arany, a kecskéé 8 arany, a juhoké 3 arany. Hány darabot vett mindegyik állatból? Oldd meg nyers erővel (azaz a lehetséges esetek végigpróbálásával) a feladatot!
- Írj programot, ami kiírja egy pozitív, egész szám osztóinak a számát!
- Írj programot, ami ki tudja számolni a következő sorozat n-edik elemét:
x0=2;xi=2·xi-1+5. - Írj programot, amely hatványozni képes! Kérdezze meg az alapot (valós) és a kitevőt (egész), és írja képernyőre a hatvány értékét!
- Gyors hatványozás. A hatványozás az egyszerű ciklusnál gyorsabban is elvégezhető, mivel az
x8=x4·x4,x4=x2·x2ésx2=x·xstb. miatt például a nyolcadikra hatványozáshoz mindössze három szorzásra van szükség. A következő megfigyelést tehetjük:xn=(x2)n/2, hanpáros, ésxn=x·xn-1, hanpáratlan.
Megoldás
#include <stdio.h> int main() { int i; for (i=0; i<16; ++i) { double alap = 2; double hatvany; int kitevo = i; hatvany=1; while (kitevo > 0) { if (kitevo % 2 == 1) { hatvany=hatvany * alap; kitevo--; } else { alap = alap * alap; kitevo/=2; } } printf("%g\n", hatvany); } return 0; } - Newton módszere a köbgyök számítására azon alapszik, hogy ha van egy tippünk a szám köbgyökére, akkor
szám/tipp2+2·tipp ───────────────── 3jobb közelítés. Írj az előadáson bemutatott „Hérón módszere” programhoz hasonlót köbgyök számítására!Megoldás
#include <stdio.h> #include <math.h> int main() { double szam, tipp; szam = 512; tipp = 1; while (fabs(tipp-szam/tipp/tipp) > 0.1) tipp = (szam/(tipp*tipp) + 2*tipp)/3; printf("%g\n", tipp); return 0; } - Az e=2,7182818… matematikai konstans előállítható az alábbi képlettel:
1 1 1 1 1 e = ── + ── + ── + ── + ── + … 0! 1! 2! 3! 4!Írj programot, amely kiszámolja ezt az első 20 taggal! A faktoriális nagy szám lehet. Tárold aztdoubletípusú változóban. (Tipp: ha ciklusban ciklust alkalmaztál, próbáld meg egyszerűsíteni a megoldásodat. Elég egyetlen egy ciklus!)Megoldás
#include <stdio.h> int main() { double e; /* e tárolása */ double fact; /* Faktoriális tárolása */ int i; /* Ciklusváltozók */ e=0; fact=1; /* Faktoriális kezdőértéke legyen 1 */ for(i=1; i<20; i=i+1) { e = e + 1/fact; /* Hozzáadjuk e-hez */ fact=fact*i; } printf("e=%f",e); /* Kiírjuk */ return 0; } -
John Wallis, angol matematikus az alábbi képletet adta a π
kiszámítására:
π 2·2 4·4 6·6 8·8 ─ = ─── · ─── · ─── · ─── · … 2 1·3 3·5 5·7 7·9
Ismerd fel a szabályosságot a sorozatban! Írd át a faktoriálist számító programodat úgy, hogy ezt a szorzatot számítsa ki! Próbáld ki a programot úgy, hogy a szorzat első 10, 100, 1000 tényezőjét veszed figyelembe!Megoldás
#include <stdio.h> int main() { double pi; /* pi tárolása */ int i; pi=1; i=2; /* 2-től indul */ for (i=2; i<10000; i=i+2) /* kettesével */ pi = pi * i * i / ((i-1)*(i+1)); /* a képlet */ /* Kiírásnál szorozzuk még kettővel a képlet miatt */ printf("%f", pi*2); return 0; } -
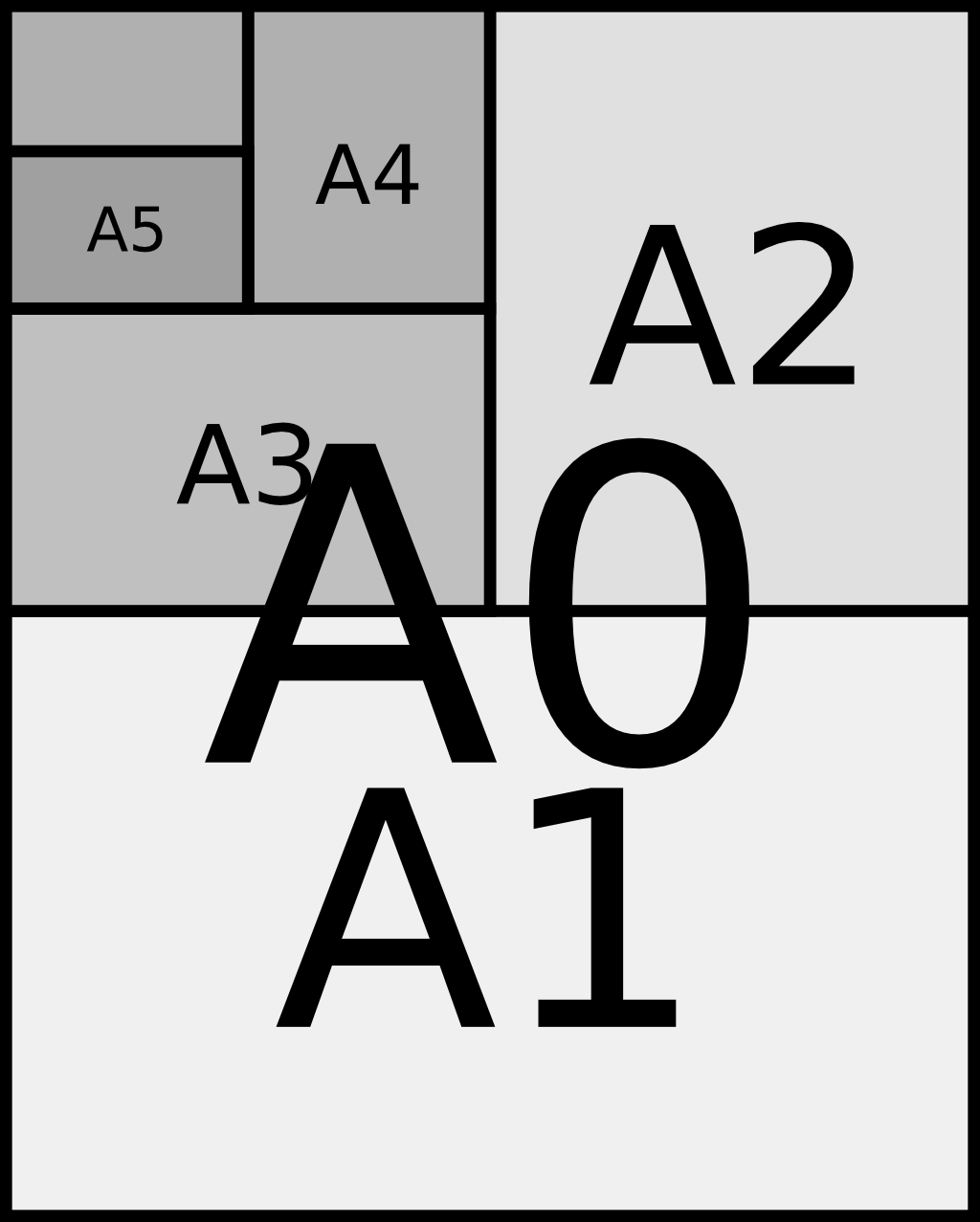 Egy A/0-s, poszter méretű lap területe 1 m2; a szélessége a magasság √2-ed része.
Az A/1-es lap ebből úgy keletkezik, hogy a
rövidebb oldalával párhuzamosan középen kettévágjuk (vagyis a hosszabbat felezzük). Az A/2-es az A/1-eshez viszonyul ugyanígy stb.
Írj programot, amelyik kiszámolja és kilistázza ezeket a papírméreteket A/0-tól A/6-ig! A program az összeset álló változatban
írja ki, ne fekvő tájolással! Pl. az A4-es állóban: 210×297 mm.
Egy A/0-s, poszter méretű lap területe 1 m2; a szélessége a magasság √2-ed része.
Az A/1-es lap ebből úgy keletkezik, hogy a
rövidebb oldalával párhuzamosan középen kettévágjuk (vagyis a hosszabbat felezzük). Az A/2-es az A/1-eshez viszonyul ugyanígy stb.
Írj programot, amelyik kiszámolja és kilistázza ezeket a papírméreteket A/0-tól A/6-ig! A program az összeset álló változatban
írja ki, ne fekvő tájolással! Pl. az A4-es állóban: 210×297 mm.
(A matek: mekkora ez alapján egy A/0-s lap? Legyen h a lap magassága, w pedig a szélessége! Tudjuk, hogy T=w·h, és azt is, hogy w=h/√2. Ebből T=h·h/√2, amibe az 1 m2-t is behelyettesíthetjük. 1=h·h/√2, √2=h·h, h=√√2. A szélessége pedig w=1 m2/h.)Megoldás
#include <stdio.h> #include <math.h> int main() { /* Változók */ int a; /* Papír méret: A0-A6 */ double a_old,b_old,rovid,hosszu; /* Oldalak */ a=0; /* A méretezés A0-tól indul */ a_old = sqrt(sqrt(2)); /* A0-s papír egyik oldala */ b_old = 1/a_old; /* A0-s papír másik oldala */ /* Ciklus A0-tól A6-ig */ while (a<=6) { /* Megnézzük melyik a rövidebb és melyik a hosszabb oldal */ if (a_old<b_old){ rovid=a_old; hosszu=b_old; } else { rovid=b_old; hosszu=a_old; } /* Kiírjuk a-t, a rövidebb és a hosszabb oldalt */ /* 1000-el szorozva, hogy milliméter legyen az egység */ printf("A%d papir: %fmm x %fmm\n",a,rovid*1000,hosszu*1000); /* A nagyobbik oldalt felezzük */ a_old = hosszu/2; b_old = rovid; /* Következő méret */ a=a+1; } return 0; }

