„és”: mindkét
feltétel teljesül
/* 3-mal és 5-tel is osztható */
if (szam%3 == 0 && szam%5 == 0)
printf("fizzbuzz\n");
Vigyázat! Melyik feltétel is teljesül 15-nél???
A feltételek átfedése miatt nem mindegy, melyiket használjuk melyik következményeként és alternatívájaként. Ha együtt nem teljesülnek, még mindig lehet, hogy külön-külön igen. Nem lenne jó itt felsorolni az összes rossz megoldást, és megmagyarázni mindegyikről, hogy mi a bajuk – az egy egyszerű nyomkövetéssel észrevehető. Mindenki kipróbálhatja magának!
Azért szerepel itt ez a példa, mert
kedvenc kérdés szokott lenni az állásinterjúkon, és meglepő,
hogy mennyiszer elrontják a jelentkezők.
(Lásd
itt és
itt.)
Hogyan függenek össze a feltételek? Hogyan kell egymásba tenni a vezérlési szerkezeteket?
Jó-e az, ha leírjuk a három vizsgálatot (3-mal, 5-tel, mindkettővel), mindenhova közé else-t téve?
Észre kell venni, hogy a feladat szövegében említett három eset igazából négyet jelent, amelyek pedig átfedik egymást.
#include <stdio.h>
int main()
{
int szam;
for (szam=1; szam<=20; szam=szam+1)
if (szam%3 == 0 && szam%5 == 0)
printf("fizzbuzz\n");
else
if (szam%3 == 0)
printf("fizz\n");
else
if (szam%5 == 0)
printf("buzz\n");
else
printf("%d\n", szam);
return 0;
}
Mivel minden feltétel igaz és hamis ágában csak egy
további utasítás van (egy következő if is
egy utasításnak számít), ezért itt nem volt szükség
az utasítások {} blokkba helyezésére.
A C nyelvtani szabályai szerint az else utasítás
mindig az azt megelőző, legközelebbi if-hez
tartozik. Ha ezt módosítani szeretnénk, az természetesen lehetséges,
az utasítások megfelelő {} blokkba helyezésével. Így:
if (feltétel1) {
if (feltétel2)
printf("akkor, ha feltétel1 és feltétel2");
} else
printf("akkor, ha nem feltétel1");
Sokan egyébként az önálló utasításokat is blokkba teszik, és nem írnak a fentihez hasonló kódot. Néha hosszabb kicsit úgy, de sok előnye van.
Összesítsük a rendeléseket!
Írjunk programot, amely összegzi a fogyasztásunkat: a felhasználótól kapott pozitív, egész számokat összegez. Addig, amíg −1-et nem kap.
+ 3
+ 1 = ?
Összegzés tétele
összeg=0 akkumulátor
CIKLUS AMÍG van még szám, ADDIG
szám = következő elem
összeg = összeg+szám
CIKLUS VÉGE
Az „akkumulátor” változó az, amelyikben összegyűlik, akkumulálódik az eredmény. Ezt először nullázzuk, utána minden feldolgozott számot hozzáadjuk. Minden iteráció végén az addig látott számok összegét fogja így tartalmazni. Ha esetleg egyszer sem ment volna be a ciklusba, akkor pedig nullát.
A végjeles sorozat kezelése: a beolvasás helye
- A ciklus feltétele ez lesz: AMÍG szám ≠ −1, …
- Ez a beolvasott számtól függ → már az első előtt lennie kell beolvasásnak
- De mindig kell egy új szám → a cikluson belül is
Helyes megoldás (a tétel alkalmazása)
különleges”
összeg = 0 BE: szám első CIKLUS AMÍG szám≠−1, ADDIG összeg = összeg+szám BE: szám következő (többi) CIKLUS VÉGE
Ez egy nagyon fontos rész. Itt a ciklus működését meg kell érteni! A ciklusfeltétel ellenőrzi azt, hogy a kapott szám −1-e, vagy nem. Mivel ez egy elöltesztelő ciklus, ezért ennek a feltételnek az ellenőrzése a ciklusba belépés előtt fog megtörténni. Ez azt jelenti, hogy a ciklus első elérésekor már rendelkeznünk kell egy számmal, ami a felhasználótól származik, vagyis kell lennie egy beolvasásnak a ciklus előtt.
Namármost, ha a feltétel igaz, akkor bekerül a végrehajtás a ciklus belsejébe. Ilyenkor éppen van egy számunk, amit a billentyűzetről kaptunk, és ami nem −1, ezért azt hozzá kell adnunk az összeghez. Itt azt általánosan megfogalmazott összegzés tételét át kell alakítanunk a jelenlegi, konkrét feladatunkhoz, hiszen a ciklustörzs nem egy beolvasással kezdődik. Helyette az összeadással, mert a számunk már megvan.
A ciklustörzs egy újabb beolvasással végződik. Ami első ránézésre olyan, mintha a következő beolvasott számmal már nem csinálnánk semmit, de ez nincs így! A ciklustörzs végrehajtása után a vezérlés újra a ciklusfeltétel ellenőrzéséhez kerül. Ilyenkor már az új számot fogja ellenőrizni a feltétel újbóli kiértékelése – és ha igaznak adódott, vagyis ha a szám nem −1, akkor már az új szám fog az összeghez hozzáadódni. A ciklustörzs végén álló beolvasás a következő iteráció számára készíti elő a terepet. Vegyük észre, hogy ilyenkor a „terep” pont ugyanúgy néz ki, mint az első végrehajtás előtt. Van egy számunk, amit meg kell vizsgálni, hogy −1-e, és ha nem, akkor hozzáadni az összeghez.
A fentiek végiggondolását kezdő és haladó programozóknak is ajánljuk. Ennek a problémának ez A Szép Megoldása.
nem egyenlő
#include <stdio.h>
int main()
{
int osszeg, szam;
printf("Kérem a számokat, -1: vége\n");
osszeg=0; // elején nulla
scanf("%d", &szam);
while (szam!=-1) {
osszeg=osszeg+szam; // ha van szám, hozzáad
scanf("%d", &szam);
}
printf("Összeg: %d\n", osszeg);
return 0;
}
„vagy”: valamelyik
feltétel teljesül
(elég az egyik)
#include <stdio.h>
int main()
{
int db, szken;
char c;
db=0;
szken=scanf("%c", &c);
while (szken==1) { // amíg nincs vége
if (c=='e' || c=='E')
db+=1; // ha megfelel, növeli
szken=scanf("%c", &c);
}
printf("%d darab e betű volt.\n", db);
return 0;
}
A programban kihasználjuk azt, hogy a scanf() jelzi
a beolvasás sikerességét is. A kért karakteren kívül ugyanis ad még
egy számot (ezt tárolják el a szken=scanf(...) sorok),
amelynek az értéke 1, ha sikerült az egy karakter a beolvasása.
A program a két feltételét (kis „e” betű-e, nagy „E” betű-e) VAGY kapcsolatba hozva használtuk. Ez azt jelenti, hogy bármelyik megfelel számunkra. Akár kis „e” betű van, akár „E” betű, a számlálót megnöveljük. A pongyolán megfogalmazott feladatkiírás szólhatna úgy, hogy „számoljuk meg a kicsi és a nagy E betűket” – hiába tudjuk, hogy nem lehet egy betű egyszerre kicsi és nagy is.
A programok írásakor a logikai VAGY és logikai ÉS kapcsolatok közötti különbséget mindig pontosan át kell gondolni. Azért fontos ez, mert a köznapi beszédben a kettőt sokszor pont fordítva használjuk. Például elhangozhat egy tankörben a következő mondat: „Tegye fel a kezét, aki Budapesten és Debrecenben született!” Nyilvánvaló, hogy senki nem születhetett egyszerre Budapesten ÉS (logikai ÉS) Debrecenben. Egyszerűen csak ezt a gondolatot rövidítjük: „Tegye fel a kezét mindenki, aki Budapesten született, és tegye fel a kezét az is, aki Debrecenben született!” A matematikailag, és ezért a programjainkban is korrekt változat élő beszédben szokatlanul hangzana: „Tegye fel a kezét mindenki, aki vagy Budapesten, vagy Debrecenben született!”
Melyik a legmagasabb rakéta?
Olvassunk be a billentyűzetről a magasságokat! Hány darabot? Kérdezzük a felhasználótól az elején! Melyik volt a legnagyobb közülük?
Szélsőértékkeresés tétele
legnagyobb=első elem első CIKLUS AMÍG van még szám, ADDIG szám = következő elem többi HA szám>legnagyobb, AKKOR legnagyobb=szám FELTÉTEL VÉGE CIKLUS VÉGE
A maximumkeresés C kódrészlete
printf("Hány szám lesz? ");
scanf("%d", &db);
printf("1. szám: "); // maximumkeresés
scanf("%lf", &aktualis);
max=aktualis; /* az első külön! */
for (i=2; i<=db; i+=1) { /* a többit ciklusban */
printf("%d. szám: ", i);
scanf("%lf", &aktualis);
if (aktualis>max) /* nagyobb az eddigieknél? */
max=aktualis;
}
printf("Legnagyobb: %lf\n", max); // eredmény
Vigyázat! Az első „tippet” is a sorozatból kell venni! Általános esetben elvi hibás a legnagyobb=−1000 kezdetű vagy hasonló megoldás! (Ha az összes szám kisebb lenne −1000-nél, akkor hibás lenne az eredmény.)
Feladat
Kérjen a felhasználótól 10 számot, és utána írja ki őket fordított sorrendben!
Megoldás – sorminta???
int a, b, c, d, e, f, g, i, j, k;
scanf("%d", &a);
scanf("%d", &b);
scanf("%d", &c);
…
printf("%d\n", c);
printf("%d\n", b);
printf("%d\n", a);
Mire lenne itt szükség?
Az eddigi programjainkban:
- Csak néhány nevesített változóval dolgoztunk, amelyeknek mind kitüntetett szerepe volt
- Nem tudtuk azt mondani, hogy „sok”
- Csak a beérkezés sorrendjében tudtuk feldolgozni az adatokat
Ami hiányzik:
- Jó lenne egyszerre több elemet is tárolni
- Az elemeket sorszámozva hivatkozni (első szám, második szám…), mert akkor egy ciklus végigmehetne az elemeken
- Az elemeket tetszőleges sorrendben elérni, mert akkor kiírhatnánk fordított sorrendben
A tömb elemeit csak egyesével lehet kezelni.
int a[10], b[10]; a=b;
for (i=0; i<10; i+=1) a[i]=b[i];
Az a=b értékadás helytelen voltának mélyebb okai vannak.
Erről később lesz szó.
A tömb méretét meg kell adni a program írásakor.
scanf("%d", &db);
int tomb[db];
/* „elég nagy” */ int tomb[];
A C nyelv újabb változata (C99) elfogadja azt, ha a tömb méretét változóval
adjuk meg, mint fent a scanf()-es példában. A régebbi, C89-es,
illetve C90-es változatban ez még nem volt lehetséges. Ez más programnyelvek
(Pascal, Java, …) esetén is eltérően szokott működni. Erről később részletesen
lesz szó – egyelőre a tömbökre, mint fix méretű tárolókra gondoljunk.
A nem megadott méretű tömb (üres szögletes zárójel) viszont nem működik
semelyik fordítóval, és így nagyon súlyos hibának számít!
| kifejezés | jelentés |
|---|---|
3.14 |
tizedespont, a π közelítő értéke vessző, elválasztás, pl. pow(3, 14)=314 |
x==y |
vizsgálat: x egyenlő-e y-nal értékadás: x legyen egyenlő y-nal |
x=b |
x vegye fel a b változó értékét x legyen a b betű karakterkódja |
x=1 |
x legyen 1 x legyen az 1-es számjegy karakterkódja |
printf("%d", 65) |
írd ki 65-öt, mint szám: "65" írd ki a 65-ös kódú karaktert: "A" |
"a" |
szöveg (sztring), amely egy betűt tartalmaz egyetlen karakter |
If blue is the sky…
Az értékadás és az egyenlőségvizsgálat keverése miatt gyakran szokták
tanácsolni, hogy a feltételeket fordítva írjuk.
Így nem lehet összekeverni a kettőt, hiszen ebben a kódrészletben
= értékadás használata esetén szintaktikai hibát kapunk,
ami fordítási hibához vezet. Sajnos a fordított feltétel az olvashatóságot
csökkenti, néha zavar a kód megértésében. Ezért mi nem javasoljuk a használatát.
A programozó folklór egyébként ezt a stílust Yoda-feltételnek
nevezi, mert Yoda az eredeti Csillagok háborúja szinkronban így beszél (pl.
„if blue is the sky”-t mond „if the sky is blue” helyett.)
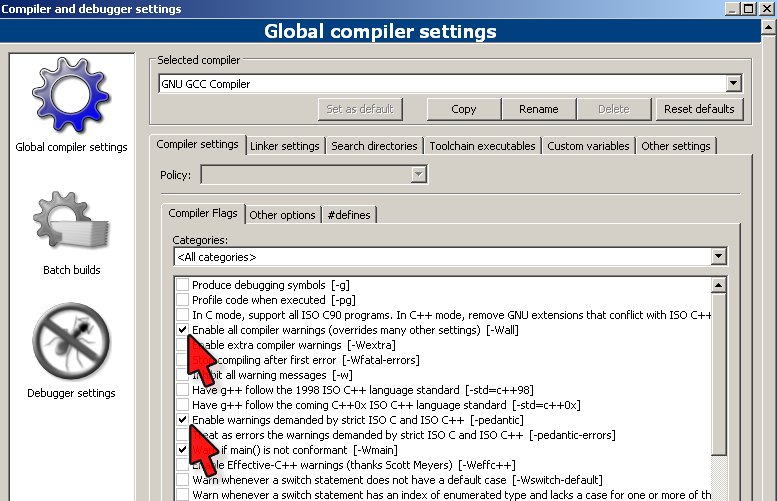
- Enable all compiler warnings (-Wall)
- Enable warnings demanded by strict ISO C (-pedantic)
A Code::Blocks Settings menüjében
találunk egy Compiler and debugger… menüpontot. Ezt
megnyitva a fordítóprogram beállításaihoz jutunk. A fent
látható két opciót nagyon erősen javasolt
engedélyezni az otthoni gépeteken. Ilyenkor ugyanis a
fordító minden gyanús, szokatlan kódrészletre figyelmeztetést
ad (-Wall), illetve a nem szabványos, esetleg más fordítókkal
nem működő nyelvi fordulatokat nem engedi használni (-pedantic).
Ezeket beállítva sokkal hatékonyabb, könnyebb a tanulás
és a gyakorlás! Például az előbb említett x=y
és x==y összekeverésére is a legtöbbször figyelmeztetni
tud.
double pi = 3.14; // inicializált változó int i, osszeg; // inicializálatlan változó
Ha nem kap kezdeti értéket, inicializálatlan lesz → memóriaszemét
A lentiek jelentik azt, hogy görcsösen adjunk kezdeti értéket
minden változónak, akkor is, ha felesleges! Például egy ciklusváltozót felesleges
inicializálni a létrehozásakor, hiszen a for() fejlécében úgyis
fog értéket kapni. Egy összegzést végző programrész osszeg=0 utasítását
is érdemes a ciklus elé tenni közvetlenül, hiszen ahhoz a programrészlethez
tartozik logikailag!
Az inicializálatlan változók
- Súlyos hiba egy inicializálatlan változó értékét használni!
- Lehet, hogy nulla, lehet, hogy nem
- Lehet, hogy mindig más az értéke, lehet, hogy nem
- Lehet, hogy működik a program, lehet, hogy nem
- Misztikus, követhetetlen hibajelenségek!
Ezt a kódrészletet mindenki ki tudja próbálni a saját gépén. A legmeglepőbb dolgok történhetnek, mivel a működése az inicializálatlan változók miatt nem definiált.
#include <stdio.h>
int main()
{
int t[15]; /* inicializálatlan */
int i;
for (i=0; i<15; i+=1)
printf("%d\n", t[i]);
return 0;
}
Túlindexelés
- A C nem ellenőrzi a megadott tömbindexeket
int t[10]tömb túlindexelése:t[-1], t[10], t[234]- Helyes indexek:
t[0]…t[9]
- Helyes indexek:
- Misztikus hibák, elvesző változóértékek, lefagyó programok
- Ezért a tömbök túlindexelése is súlyos hiba!
Az indexhatárok nem ellenőrzésének az oka egyszerű: a hatékonyság. A C nyelv sok modern programozási nyelvvel ellentétben arra való, hogy a lehető leggyorsabban futó programokat írjuk vele. A helyesen megírt programban sehol nincsen tömb túlindexelés, ezért felesleges is lenne a program futása közben ellenőrizni, hogy van-e benne ilyen hiba! A helyes program írása így aztán nem másnak a feladata, mint a programozónak.
„Ki itt belépsz, hagyj fel minden reménnyel.”
Nem definiált működés: ha valami nincs meghatározva a C szabványban, akkor annak hatására akármi is történhet. Nincs garantálva semmi.
Ezt is érdemes kipróbálni.
#include <stdio.h>
int main()
{
double t[10];
int a=1, b=2, c=3;
printf("a=%d\nb=%d\nc=%d\n", a, b, c);
/* túlindexelés */
t[-1]=0.2;
t[10]=0.3;
printf("\n");
printf("a=%d\nb=%d\nc=%d\n", a, b, c);
return 0;
}
