Útravaló
Tartalom
- Versenyek
- Mit csináltunk a félévben?
- Pár furcsaságot is terveztünk
- Komplex példa: táblázatkezelő
- Egy táblázat anatómiája
- Kifejezések értelmezése (parsing)
- Matematikai kifejezések kiértékelése
- A nyelvtani szabályok
- Formális nyelvtanok – az EBNF
- Matematikai kifejezés – számok összege
- Matematikai kifejezés – precedencia I.
- Matematikai kifejezés – precedencia II.
- Matematikai kifejezés – zárójelek
- A rekurzív alászálló értelmező
- Az kiértékelő megírása I.
- Az kiértékelő megírása II.
- Az kiértékelő megírása III.
- Kifejezés kiértékelő működés közben
- A cellák kiértékelése
- A cellák kiértékelése
- A körkörös hivatkozás
- A táblázat reprezentálása: az adatszerkezet
- Egy cella kiszámolása
- A cella módosítása
- Fordítási függőségek csökkentése
- Táblázatkezelő DEMO
- Epilógus
- http://infoc.eet.bme.hu/
typedef void Ize, Semmi;- Mit ír ki?
- Mit ír ki?
#definetrollkodás
1 Versenyek
Nagyházi szépségverseny

- Beküldés:
infoc@eet.bme.hu, NEPTUN kóddal - Screenshot a nagyháziról (egy jellegzetes jelenetről)
- Min. 3, max. 5 soros leírás
Programozási verseny
- Boros László kezdeményezése
- Vizsgaidőszak vége felé (?)
- Nevezés egy otthon elkészített programmal
- Részletek később!
2 Mit csináltunk a félévben?
2. Nézd meg, világít-e a lámpa.
Ha igen, ugorj a 7. pontra.
3. Nyomd meg az m↓T gombot.
4. Nyomd meg az A←B gombot.
5. Nyomd meg a T↑B gombot.
6. Ugorj a 2. pontra.
7. Kész, az eredmény A-ban.
while (b != 0) {
t = a%b;
a = b;
b = t;
}
Gépeket terveztünk, amelyek adott feladatot megoldanak. Ezen gépek szöveges leírását adtuk C nyelven.
Megtanultunk algoritmizálni, amihez az eszközkészletünk:
- változók: szükséges információ tárolása,
- feltételes elágazások és ciklusok: megadják a megoldás menetét,
- függvények: újrahasznosítható programrészletek egy apró feladat megoldására,
- modulok: újrahasznosítás nagy léptékben.
Megismertünk adatszerkezeteket (tömbök, listák, fák):
- a komplex valóság pontosabb modellezésében segítenek,
- hatékonyan használják ki a gépünk erőforrásait.
„Mellékesen” megtanultuk a C nyelvet.
3 Pár furcsaságot is terveztünk
int fakt(int n) {
if (n==0)
return 1;
else
return n*fakt(n-1);
}
Gépben gép:
rekurzió
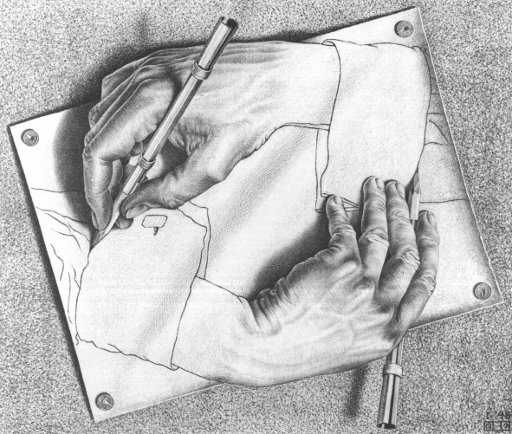
5 Egy táblázat anatómiája
| A | B | C | D | |
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 |
Kihívások:
- A képletek értelmezése.
- A keretszhivatkozások feloldása.
Gondoljuk meg: a fizetendő összeg kiszámolásakor a képlet hivatkozik az egyes italok árára (amiket megszoroz a fogyasztott mennyiséggel). Az italok árai további cellákra hivatkoznak (összetevők ára és mennyisége). Az igazi problémát az jelenti, hogy nagyon nehéz feladat megtalálni azt a bejárási sorrendet, amelyen végighaladva csupa már kiszámolt celleértéket használunk csak fel.
A jelen esetben ez azt jelentené, hogy előbb kiszámoljuk az egyes italok árait, majd ezután számoljuk ki a fizetendő összeget. Csakhogy a Long Island Ice Tea egy jóval későbbi cellában helyezkedik el, mint a fogyasztás, így előre-hátra kéne ugrálni a cellák között.
Egy összetett lapon annyira bonyolult összefüggések lehetnek az egyes cellák között, hogy a kiszámolás útvonalának a feltérképezése annyira nehézzé válik, amit már nem érdemes leprogramozni. Ehelyett azt választjuk, hogy elindulunk a bal-felső cellától és jobbra-lefelé haladva sorra vesszük a cellákat.
Ha egy cella hivatkozik egy másik értékére, akkor elugrunk oda, és megnézzük azt az értéket. Ha az is hivatkozik egy másikra, akkor tovább ugrunk egészen addig, amíg olyan cellákig nem érünk, amelyek rögtön kiértékelhetőek (pl. egy szám vagy csupa számokból álló képlet van bennük, vagy már korábban kiszámoltuk az értéküket).
Előfordulhat egy olyan eset, amikor egy cella hivatkozik egy másik cella értékére, ami viszont hivatkozik az elsőre. Például az A3 cella képlete: A3 = B4 * 2, míg a B4-é: B4 = 123 + A3. Az ilyen jellegű hivatkozások nem oldhatóak fel, nem tudjuk meghatározni az értéket. Ugyanakkor a programunk végtelen ciklusba kerülhet miattuk, ezért fel kell derítenünk, vagy a számolás során észre kell vennünk az ilyen csapdákat. Ráadásul egy ilyen, ún. körkörös hivatkozás előfordulhat több lépésben is – például az A3 hivatkozik a B4-re, ami hivatkozik a C8-ra, ami az A7-re, ami az A3-ra. A programnak ezeket is észre kell vennie, hiszen itt is ugyanúgy előállna a végtelen rekurzió.
Ezeket a problémákat kell megoldania a programunknak.
7 Matematikai kifejezések kiértékelése
Matematikai kifejezések
- Postfix alak:
4 5 7 + * - Prefix alak:
* 4 + 5 7 - Infix alak:
4 * (5 + 7)
Ezek mind ugyanazt jelentik.
Infixes alak: 4 * (5 + 7)
Ezt összetett feladat értelmezni: zárójelek, precedenciaszabályok, …
A nyelvi elemzés (parse, parsing) „Helló világ”-ja a négy alapműveletet és a zárójeleket ismerő matematikai kifejezések értelmezése.
Furcsa vagy nem, a legbonyolultabb a fenti három közül a hétköznapi infixes
alak, amely esetén az operátort a két operandus közé tesszük. Itt megszoktuk
azt, hogy a műveleteknek precedenciája van. Például a szorzásé magasabb,
mint az összeadásé. Hogy az 5+7 összeget szorozzuk 4-gyel,
a kifejezésben zárójelezni is kell azt.
A postfixes alak esetén az operandusok után van az operátor.
Minden operátor az előtte lévő két operandusra vonatkozik. Pl.
4 5 7 + *, a +
jel az előtte álló 5-ösre és 7-esre. Ezt lehetne zárójelezni is, de felesleges,
hiszen mindig tökéletesen egyértelmű. Nincsen szükség precedenciaszabályokra sem.
Példa egy bonyolultabb képletre:
(3+4)*(5+6) = 3 4 + 5 6 + *
A prefixes alak esetén az operátor az operandusok előtt van. Ez egyrészről lehetne a postfixes visszafelé, másrészről viszont szokás mindig zárójelezni. Ugyanis zárójelezés esetén könnyedén tudjuk azt is jelezni, ha egy operátornak kettőnél több operandusa van:
(+ 4 5 6)
Ez a 4, 5 és 6 számok összege. Ezt infix alakban le sem tudjuk írni, csak két külön összeadással – amely egyrészről ugyanazt jelenti, másrészről viszont korántsem ugyanaz:
4+5+6 = (+ 4 (+ 5 6))
8 A nyelvtani szabályok
Kezdetnek próbáljuk megfogalmazni, hogy néz ki egy egész szám:
Decimális egész szám
- Egy szám legalább egy számjegyből áll.
- Egy számjegy a '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' szimbólumok valamelyike.
- Ha a szám több számjegyű, akkor a legelső számjegy nem lehet nulla.
2. előadás
A fenti, szabad nyelvi leírás nehezen áttekinthető és nem formális, ami nehezíti az algoritmizálást.
9 Formális nyelvtanok – az EBNF
Az egész szám formális leírása EBNF alakban:
szám ::= számjegy | (számjegy_nemnulla számjegy+) számjegy_nemnulla ::= '1'|'2'|'3'|'4'|'5'|'6'|'7'|'8'|'9' számjegy ::= '0'|számjegy_nemnulla

ahol
::=egy nyelvtani szabály definíciója'c'egy tényleges karakter a szövegben|opció (vagy az egyik elem van ott, vagy a másik)+egy, vagy több ugyanolyan elem()egy együtt kezelt egység (ua. mint algebrában)- egymás után írt szimbólumok pedig egymást kell kövessék a szövegben.
Többféle EBNF alak létezik, mi most a W3C konzorcium szabványát használjuk.
10 Matematikai kifejezés – számok összege
összeg ::= szám (('+' | '-') szám)*
A * tetszőleges számú (akár 0) ismétlést jelent.
A minta illeszkedik (match) ezekre a példákra:
2
234 + 14
1278 - 897
788 + 567 - 34
11 Matematikai kifejezés – precedencia I.
Fontos a precedencia: hogyan tudjuk bevezetni a szorzást/osztást?!
Nem vezethetjük be a '+' és '-' alternatívájaként:
kifejezés ::= szám (('+' | '-' | '*' | '/') szám)*
Így nem érvényesül az, hogy pl. a
2 + 3 * 6kifejezésben a szorzás a 3-ra és a 6-ra vonatkozik: 2+(3*6).
12 Matematikai kifejezés – precedencia II.
Ötlet: legyen a szorzás és osztás egy különálló egység, így azokat egyben kezeli az értelmező.
Ez azt jelenti, hogy egy új szabályt vezetünk be a szorzás és osztás számára.
kifejezés ::= összeg
összeg ::= szorzat (('+' | '-') szorzat)*
szorzat ::= szám (('*' | '/') szám)*
A szabályok jelentése a fentiek alapján a következő:
- A kifejezésünk egy összeg
- Az összeg szorzatokból áll (szorzatok összege)
- A szorzat pedig számok szorzata.
Nézzük meg, hogy hogyan értékelődik ki a 2+3*6:
2 + 3 * 6
szám szám szám
\___________/
szorzat szorzat
\________________________/
összeg
- A kifejezés elejére egy szorzatot próbál illeszteni az összeg kifejezés alapján.
- Egy szorzat egy számmal kezdődik – ez rendben van: '2' egy szám.
- Utána következhetne egy '*' vagy '/' és egy szám – ez nincs itt meg, hiszen '+' jön, de nem baj, mert egy szorzat lehet egy szám önmagában.
- Folytatjuk az összeg értelmezését és találunk is egy '+'-t, tehát megint egy szorzatnak kell jönnie.
- Ott egy szorzat: "3*6", amit tehát szorzatként ismerünk fel! Az eredményét összeadjuk az összeg első tagjával.
Figyeljük meg, hogy a fenti nyelvtan továbbra is leírja az összes esetet, amit az összeadás/kivonás vizsgálatakor megnéztünk, hiszen a szorzat bármikor leegyszerűsödhet egy egyszerű számmá, amivel visszakapjuk az eredeti, egy szabályból álló nyelvtant.
13 Matematikai kifejezés – zárójelek
Ami egy kifejezés értelmezését bonyolulttá teszi, az a zárójel!
Minden zárójelen belül egy új kifejezés van: úgy kell értelmezni, mint az egészet, és önálló egységként kell kezelni. Ezen felül: tetszőleges mélységben egymásba ágyazható kifejezéseket kell értelmeznünk.
Megoldás: új szabályt kell bevezetni a zárójel lekezélésére – ezzel megoldjuk, hogy egy egységként legyen lekezelve (precedencia). Mi lehet egy zárójelpáron belül? Egy új matematikai kifejezés, vagyis a legalacsonyabb szabályunk! Ez egy rekurzió.
Új szabályt kell bevezetni a zárójel kezelésére:

kifejezés ::= összeg
összeg ::= szorzat (('+' | '-') szorzat)*
szorzat ::= tényező (('*' | '/') tényező)*
tényező ::= szám | zárójeles
zárójeles ::= '(' kifejezés ')'
Így értelmezhetővé válnak az alábbi alakok is:
nyelvtan!
2 + 3 * (4 - 8 * 2) 12 * ((3 - 4) * 14)
Már csak ki kéne találni, hogy hogyan tudunk olyan programot írni, amit egy ilyen nyelvtan szerint kiértékel!
14 A rekurzív alászálló értelmező
Minden szabálynak feleltessünk meg egy függvényt. A függvény átveszi az értelmezendő sztring címét, amit a futása során a sikeresen felismert szakasz végére állít át. (Ha nem ismert fel semmit, akkor nem változtatja meg). A függvény a visszatérési értéke logikai típusú, ami igaz, ha sikeresen felismert egy szakaszt, és hamis, ha nem történt illeszkedés. Minden függvény ezentúl paraméterként átvett változók címébe tölti a felismert szakasz értelmezésével kapcsolatos eredményeit.
descent
parser
Minden szabályhoz egy függvény:
int szabaly(char **szoveg, ……… *eredmeny);
Az illesztő függvény általában így néz ki (ez most számjegyet illeszt):
int szamjegy(char **szoveg, char *szamjegy) {
char *ptxt = *szoveg; // munkaváltozat
if (ptxt[0]>='0' && ptxt[0]<='9') { // számjegy?
*szamjegy = ptxt[0];
*szoveg = ptxt+1;
return 1; // illeszkedik :)
}
else
return 0; // nem illik rá :(
}
Az illesztő függvény átvesz egy pointert, amely az értelmezendő szövegrészre mutat. Ha sikeres az illesztés, akkor igazzal tér vissza, és lépteti ezt a pointert, mégpedig az illeszkedő szövegrész utánra. (Ezért veszi át cím szerint.) A függvény további paraméterei pedig arra valók, hogy az illesztés során előálló adatokat oda írja a függvény.
Az illesztés menete a fenti példafüggvényre (amely egy számjegyet próbál illeszteni a szövegrészre) a következő:
- Készítünk egy munkaváltozatot
ptxt-be. Ahogy haladunk ennek a szabálynak a feldolgozásával, ezzel dolgozunk. - Megpróbáljuk számjegyként értelmezni az aktuális karaktert.
- Ha sikerült, akkor
- a paraméterként kapott változóba írjuk az eredményt,
- léptetjük az értelmezett szöveget,
- igazzal térünk vissza.
A ptxt változóra bonyolultabb szabályok
esetén van igazán szükség. Mert ha a szabály illesztése sikertelen, akkor
a *szoveg mutatót nem állítjuk el! Ha sikeres, akkor viszont
beállítjuk a soron következő értelmezendő szövegrészre.
Nagyon fontos, hogy csak akkor változtatja meg a szövegre mutató pointer értékét, ha sikeres volt az értelmezés. Ez biztosítja ugyanis a összefűzhetőséget, amit az alábbiakban fogunk megvizsgálni.
A lenti kódrészletekben „………” helyére mindig az elemzés eredményének tárolási címét kell tenni. Hogy ez mit jelent, az az adott szabálytól függ.
15 Az kiértékelő megírása I.
A leírt függvényalak könnyűvé teszi a nyelvtanok algoritmizálását.
Opcionalitás
'-'? szám
Vagyis ott vagy van egy elem, vagy nincs:
char *szoveg = "-223";
if (szabaly_minusz(&szoveg, ………)) {
/* sikeres illeszkedés feldolgozása */
}
/* további részek feldolgozása */
Az opcionális elem feldolgozásának menete a következő.
Ha a szabaly() az illeszkedése sikeres volt,
akkor a szoveg mutató a
soronkövetkező, értelmezendő karakterre mutat, és a szabaly() „………”-al jelölt
argumentum(ok)ban visszaadta az illesztett rész feldolgozott eredményét.
Ilyenkor, kilépve az if blokkból a soronkövetkező szabályok már a
léptetett mutatót kapják meg.
Ha nem történt értelmezés, akkor egyszerűen tovább lépünk az if-en
és a változatlan mutatót kapják a további szabályok, vagyis ugyanonnan
próbálják értelmezni a sztringet, mint ahonnan a szabaly próbálta
sikertelenül.
Tetszőleges számú előfordulás
szám ::= nemnullaszámjegy bármilyenszámjegy*
Vagyis lehet akár nulla, egy vagy sok illeszkedő rész:
char *szoveg = "223";
/* előző részek feldolgozása */
while (szabaly_barmilyenszamjegy(&szoveg, ………)) {
/* első és további illeszkedések feldolgozása */
}
/* további részek feldolgozása */
A működése hasonló a fentihez, csak a szabály
illesztése többször is megtörténik. Minden egyes sikeres illesztésnél
a szoveg pointer módosul, így a különböző
hívások eltérő szövegrészeken dolgoznak.
Legalább egyszeri előfordulás
név ::= vezetéknév keresztnév+
char *szoveg = "Kiss István Pista";
/* előző részek feldolgozása */
if (szabaly_keresztnev(&szoveg, ………)) {
/* első illeszkedés feldolgozása */
while (szabaly_keresztnev(&szoveg, ………)) {
/* további illeszkedések feldolgozása */
}
}
else
return 0; /* nincs illeszkedés! */
A *-nál előfordulhat, hogy egyszer sem lépünk be a ciklusba, de akárhány iteráció is történhet.
Ha sikeres az első illesztés (if), akkor
feldolgozzuk, és egy while ciklussal addig próbálunk
illeszteni, amíg lehet. Az eredményeket pedig fokozatosan dolgozzuk
fel a ciklusmagban.
Akár sikeres volt az illesztés, akár nem, illetve akármennyiszer illesztettünk, mindenképpen a soronkövetkező, értelmezendő karakterre mutat a pointer a ciklus alatti kódrészekben.
Opciók
megszólítás ::= 'Tisztelt' ('Hölgyem'|'Uram')
Kihasználjuk a logikai rövidzárat!
char *szoveg = "Tisztelt Uram!";
/* előző részek feldolgozása */
if (szabaly_holgyem(&szoveg, ………)
|| szabaly_uram(&szoveg, ………)) {
/* bármelyik opció teljesül, itt értékeljük ki */
}
else
return 0; /* nem illeszkedett! */
/* további részek feldolgozása */
Az opcióknál ha az első szabály sikerrel értékelődik ki, akkor a logikai rövidzár miatt a másodikat már nem is próbálja meg illeszteni! Ha pedig nem sikerült az elsőt illeszteni, csak akkor próbálja meg a másodikat.
Az if belesejébe csak akkor lépünk, ha a szabályok valamelyike
sikeresen illeszkedett. Természetesen az argumentumokként kapott értékek
alapján, vagy az egyes szabályok visszatérési értékének elmentése segítségével
ellenőriznünk kell, hogy melyik szabály illeszkedett ténylegesen.
Egymásra következés
megszólítás ::= 'Tisztelt' címzett
Itt is kihasználjuk a logikai rövidzárat!
char *szoveg = "Tisztelt Uram!";
char *ptxt = szoveg;
if (szabaly_tisztelt(&ptxt, ………)
&& szabaly_cimzett(&ptxt, ………)) {
/* illeszkedés feldolgozása */
}
else
return 0; /* nem illeszkedett! */
/* további részek feldolgozása */
Csak siker esetén értékeli ki a második szabályt, tehát az
egymásrakövetkezés ki van kényszerítve, de vigyázni kell rá, hogy ha az első
szabály illeszkedett, akkor itt odébb lett állítva a pointer, és ezért
ilyenkor kiléphetünk úgy az if-ből, hogy nem volt teljes
illeszkedés, de a pointer olyan pontra mutat, ami túl van az első még
értelmezetlen karakteren. Ezért őt vissza kell állítani sikertelen esetben
(vagy ha függvényben vagyunk, meg sem változtatni a cím szerinti paramétert,
és visszatérni HAMIS értékkel.)
16 Az kiértékelő megírása II.
Buktató: vegyes logikai kifejezések?
if ((tisztelt(&szoveg, ………) && nev(&szoveg, ………))
|| hello(&szoveg, ………)) {
/* illeszkedés feldolgozása */
}
Ha tisztelt() illeszkedik, de nev() nem, akkor megpróbálja
hello()-t illeszteni, de tisztelt() elállította a mutatót! Ilyenkor
vissza kell állítani a mutatót a szöveg elejére az ÉS kapcsolat sikertelensége esetén,
és utána lehet megpróbálni hello()-t illeszteni.
Buktató: ciklusban egymásra következés?
while (szabaly1(&szoveg, ………) && szabaly2(&szoveg, ………) {
/* illeszkedés feldolgozása */
}
Ez sem jó ötlet. Itt is megsértjük a fenti szabályokat, miszerint ha sikerül az illesztés,
léptetjük a pointert, ha nem sikerül, akkor pedig marad. Ugyanis előfordulhat, hogy
szabaly1() illeszkedik, de szabaly2() nem. Ilyenkor a teljes kifejezés
értéke hamis, és a végrehajtás nem kerül be a ciklusmagba – de a szabaly1()
elállította a mutatót!
17 Az kiértékelő megírása III.
int osszeg(char **szoveg, int *ertek) {
char *ptxt = *szoveg;
int val;
if (szorzat(&ptxt, &val)) {
int val2; char c;
while (pluszminusz_szorzat(&ptxt, &c, &val2)) {
if (c == '+') val += val2;
else val -= val2;
}
*ertek = val;
*szoveg = ptxt;
return 1;
}
return 0;
}
Az első szorzat eredményét val-ban menti el, majd ( ('+'
| '-') szorzat)* illesztést próbál csinálni az egymásrakövetkezés és a
tetszőleges sázmú ismétlődés együttes alkalmazásával, és val mindig
megváltoztatja a történtek függvényében.
Itt szükség van még egy változóra (tmp), amelyben a további
szorzat részeredményeket eltárolhatjuk, hiszen a val
értékét csak mi változtathatjuk az első illeszkedés után.
A nyelvtani szabályok alapján az elemző kód megalkotása automatizálható. Erre vannak is programok, pl. a yacc. A Spirit pedig egy olyan függvénykönyvtár, amely a C++ nyelvet egészíti ki úgy, hogy a nyelv eszközeivel EBNF-szerű kifejezéseket tudunk megfogalmazni.
18 Kifejezés kiértékelő működés közben
Példa bemenet:
3+4*5
az infoc-ről!
A teljes program letölthető erről a linkről: parser_ws.c.
Ez annyiban tud többet a fentiekben bemutatottnál, hogy bárhol elfogad
szóközöket is a kiértékelt kifejezésben (erre utal a nevében a ws szócska: whitespace).
A megvalósításában azonban mindenhol a fent bemutatottakat követi. Mivel a leírt
nyelvtanunk nem ismeri a negatív számokat, ezért csak pozitív és csak egész számokon
működik a program! Pl. 5+-3 azt fogja mondani, hogy nem tudja értelmezni.
20 A cellák kiértékelése
Térjük át a táblázatkezelő részre. A cellák kiértékelése:
- meg kell különböztetni a szöveget és a képletet tartalmazó cellákat,
- fel kell tudni dolgozni a cellahivatkozásokat,
- észre kell venni a körkörös hivatkozásokat és jelezni kell őket.
| A | B | C | |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 |
Kiértékelés menete pl. B2-re:
B2 → B1 → B5 → B4
A cellák bejárása rekurzívan történik:
kiszamol(cellacím) {
HA (van cella hivatkozás) {
kiszamol(hivatkozott cella);
}
cella érték beállítása;
}
Vagyis kiszámoljuk a hivatkozott cellák értékét, mert utána az aktuális cella értéke már megmondható. Rekurzió!
21 A körkörös hivatkozás
| A | B | |
|---|---|---|
| 1 | ||
| 2 |

A probléma a fenti kóddal az, hogy ha körkörös hivatkozás van, akkor végtelen lesz a rekurzió. Kell egy megfelelő leállási feltétel.
A megoldást az jelenti, hogy a cellabejárás során megjelöljük a cellákat, ahol jártunk már. Így ha egy cellára visszajutunk, akkor az körkörös hivatkozást jelent. Ekkor hibaüzenetet adunk a cella címének megjelölésével. Amikor egy cella értékét sikeresen kiszámoltuk, a bejelölést megszüntetjük, így „teszünk rendet” magunk után.
logikai kiszamol(cellacím) {
HA (jártunk itt) VISSZA HAMIS;
cella megjelölése; +jel
HA (van cella hivatkozás) {
HA (!kiszamol(hivatkozott cella)) VISSZA HAMIS;
}
cellaérték beállítása;
cellajelölés törlése; -jel
VISSZA IGAZ;
}
22 A táblázat reprezentálása: az adatszerkezet
Maga a táblázat egy kétdimenziós tömb:
typedef struct tablazat {
cella **adat; /* 2D din. tömb */
int szelesseg;
int magassag;
} tablazat;
A táblázat egy cellája:
typedef struct cella {
char *tartalom; /* din. sztring */
double cachelt_ertek; /* ne kelljen többször */
int kiszamolva;
int mar_jartunk_itt; /* bejáráshoz */
} cella;
cella struktúrában a kiszamolva mező azt jelenti, hogy az adott körben már meghatároztuk a cella tartalmát. Ez két okból történhetett: a bejárás során már érintettük a cellát vagy egy korábbi cella hivatkozott rá és a hivatkozás feloldásakor ugrottunk ide. Ha a kiszamolva igaz, akkor a cachelt_ertek mező tartalmazza a cella érvényes értékét.
23 Egy cella kiszámolása
int cella_kiszamol(tablazat *a_tablazat, int sor, int oszlop) {
cella *a_cella = &a_tablazat->adat[sor][oszlop];
if (a_cella->mar_jartunk_itt) return 0; // körkörös!
if (a_cella->kiszamolva) return 1; // már kész
a_cella->mar_jartunk_itt = 1;
double ertek;
if (kiertekel(a_cella->tartalom, &ertek, a_tablazat)) { // ok?
a_cella->cachelt_ertek = ertek;
a_cella->kiszamolva = 1;
a_cella->mar_jartunk_itt = 0;
return 1; // ok!
}
a_cella->mar_jartunk_itt = 0;
return 0; // hiba
}
A cella_kiszamol() hívja a kiertekel()-t:
… és a kiertekel() hívja a cella_kiszamol()-t. Kölcsönös rekurzió!
24 A cella módosítása
Csak akkor írhatunk bele, ha nem viszünk be körkörös hivatkozást:
void cella_modosit(tablazat *a_tablazat, int sor, int oszlop,
char *tartalom) {
char *regi = a_tablazat->adat[sor][oszlop].tartalom;
char *uj = (char *) malloc(strlen(tartalom) + 1);
strcpy(uj, tartalom);
/* megpróbáljuk betenni az újat */
a_tablazat->adat[sor][oszlop].tartalom = uj;
/* sikerült? */
if (cella_kiszamol(a_tablazat, sor, oszlop)) {
free(regi);
} else {
free(uj); // hiba!
a_tablazat->adat[sor][oszlop].tartalom = regi;
}
}
25 Fordítási függőségek csökkentése
Minden modul mutassa a lehető legkisebb felület!
#include "tablazat.h"
int kiertekel(char *szoveg, double *ertek,
tablazat *a_tablazat);
kiertekel függvényét ismeri a táblázatkezelő,
hiszen ez az ún. "kezdőszabály". Ez az a szabály, ami egy teljes kifejezés
szerkezetét leírja. Az egyes részleteket leíró szabályok függvényeit csak
modulon belül hívjuk, így ezeket a külvilágnak nem kell ismerniük.
Az elemző többi függvénye statikus – tehát a modulra nézve lokális.
#include "elemzo.h"
static int szokoz(char **txt) {...}
static int karakter(char **txt, char const *vals, char *talalat) {...}
static int szam(char **txt, double *val) {...}
static int cellacim(char **txt, char *oszl, int *sor) {...}
static int osszeg(char **txt, double *val, tablazat *tabla) {...}
static int szorzat(char **txt, double *val, tablazat *tabla) {...}
static int tenyezo(char **txt, double *val, tablazat *tabla) {...}
static int zarojeles(char **txt, double *val, tablazat *tabla) {...}
Miért jó, ha így csináljuk? Két okból. Egyrészt,
aki használja az elemzőt, nem kell gondolkodjon, hogy a sok számára érthetetlen
függvény közül melyiket kell hívja. Egy függvény érhető el, a kiertekel().
Másrészt a fejlécfájlt más forrásba is beillesztjük, ezért ha változik, azokat
a forrásokat is újra kell fordítani. Ha a kifelé nem mutatott részeket nem
írjuk bele, akkor az ottani változtatások miatt nem kell feleslegesen sok mindent
újrafordítani a programban.

26 Táblázatkezelő DEMO
tablazatkezelo.zip
Utasítás: kiir ---+-----------+-----------+-----------+-----------+-----------+ | A | B | C | D | E | ---+-----------+-----------+-----------+-----------+-----------+ 0 | Osszetevo | Rum | 12 | Ft/ml | | 1 | | Cola | 2 | Ft/ml | | 2 | CubaLibre | | 800 | Ft | | 3 | | | | | | 4 | | | | | | ---+-----------+-----------+-----------+-----------+-----------+ Utasítás: vizsgal c2 C2: =C0*50+C1*100 Utasítás:
28 http://infoc.eet.bme.hu/
Egy C99 függvény belsejében elhelyezhetünk egy Web címet:
#include <stdio.h>
int main() {
int i;
i = 0;
http://infoc.eet.bme.hu/
printf("Helló, InfoC!\n");
i++;
if (i<10) goto http;
return 0;
}
Ez azért van, mivel a kettősponttal egy címkét jelölhetünk meg a kódban,
ahova a goto utasítással lehet ugrani. A címke neve itt
http lesz – így az if()-fel és a
goto http-vel egy hátultesztelő ciklust valósítunk meg.
Természetsen a címkék neve egyedi kell legyen, tehát egy függvényben
csak egy http:// kezdetű címünk lehet.
29 typedef void Ize, Semmi;
A void typedef-elhető:
typedef void Ize, Semmi;
Semmi foreach(Ize *ettol, Ize *eddig, Semmi (*fv)(Ize *),
Semmi (*kov)(Ize **)) {
for (Ize *iter = ettol; iter != eddig; kov(&iter))
fv(iter);
}
Semmi intkiir(Ize *pi) {
printf("%d ", *(int *)pi);
}
Semmi intptrnovel(Ize **pi) {
++ *(int **)pi; /* here be dragons */
}
foreach(tomb, tomb+5, intkiir, intptrnovel);
30 Mit ír ki?
int main() {
int a[] = { 0, 10, 20, 30, 40, 50 };
/* drunk, fix later */
printf("%d", 3[a]);
return 0;
}
Tipp: az összeadás kommutatív: tagjai felcserélhetőek.
int main() {
int c;
c = 1["Hello"];
printf("%c", c);
return 0;
}
A sztring C-ben: csak egy karaktertömb, semmi más.
31 Mit ír ki?
#include <stdio.h>
main(t,_,a) char *a; {
return!0<t?t<3?main(-79,-13,a+main(-87,1-_,main(-86,0,a+1)+a)):
1,t<_?main(t+1,_,a):3,main(-94,-27+t,a)&&t==2?_<13?
main(2,_+1,"%s %d %d\n"):9:16:t<0?t<-72?main(_,t,
"@n'+,#'/*{}w+/w#cdnr/+,{}r/*de}+,/*{*+,/w{%+,/w#q#n+,/#{l+,/n{n+,/+#n+,/#\
;#q#n+,/+k#;*+,/'r :'d*'3,}{w+K w'K:'+}e#';dq#'l \
q#'+d'K#!/+k#;q#'r}eKK#}w'r}eKK{nl]'/#;#q#n'){)#}w'){){nl]'/+#n';d}rw' i;#\
){nl]!/n{n#'; r{#w'r nc{nl]'/#{l,+'K {rw' iK{;[{nl]'/w#q#n'wk nw' \
iwk{KK{nl]!/w{%'l##w#' i; :{nl]'/*{q#'ld;r'}{nlwb!/*de}'c \
;;{nl'-{}rw]'/+,}##'*}#nc,',#nw]'/+kd'+e}+;#'rdq#w! nr'/ ') }+}{rl#'{n' ')# \
}'+}##(!!/")
:t<-50?_==*a?putchar(31[a]):main(-65,_,a+1):main((*a=='/')+t,_,a+1)
:0<t?main(2,2,"%s"):*a=='/'||main(0,main(-61,*a,
"!ek;dc i@bK'(q)-[w]*%n+r3#l,{}:\nuwloca-O;m .vpbks,fxntdCeghiry"),a+1);
}
Hogy működik? Reverse Engineering the Twelve Days of Christmas.
Ehhez hasonló C kódokat a The International Obfuscated C Code Contest oldalon lehet találni. Ők minden évben megrendeznek egy versenyt, hogy ki tud olvashatatlanabb C kódot írni.
32 #define trollkodás
#define ever (;;)
for ever {
printf("I ♥ U\n");
}
A struct és a union szintaktikája
„vészesen” hasonlít egymásra:
struct szamok {
int i;
double d;
};
union szamok {
int i;
double d;
};

Tehát a teendők:
- Bekapcsolni a szobatárs gépét
- Megkeresni a fejlesztőkörnyezet
stdio.h-ját - Beírni az elejére:
#define struct union - Várni a hatást :D