5. gyakorlat: függvények, top-down tervezés

A betűk is csak számok a gép számára. Így aztán két karakter kivonása is értelmes művelet. Az általában használt ASCII kódtáblában egymás mellett vannak ábécé sorrendben a nagybetűk, és egy másik tartományban egymás mellett a kisbetűk. Emiatt a 'C'-'A' kifejezés 2-t ad (mivel a C és az A betű között 2 a távolság). Az 'A'-'a' kifejezés a két tartomány távolságát adja meg.

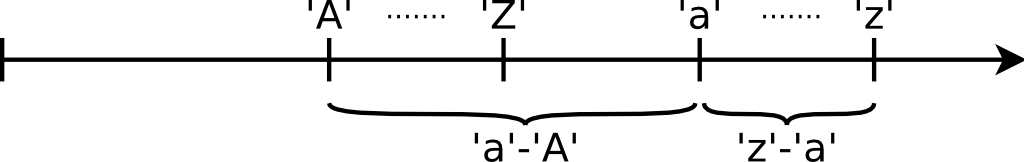
/* visszaadja a karakter nagybetus parjat, vagy sajat magat */
char nagybetu(char c)
{
    if (c>='a' && c<='z')
        return c-'a'+'A';
    return c;
}

/* visszaadja a karakter kisbetus parjat, vagy sajat magat */
char kisbetu(char c)
{
    if (c>='A' && c<='Z')
        return c-'A'+'a';
    else
        return c;
}

#include <stdio.h>

/* Igaz ertekkel ter vissza, ha a parametere egy maganhangzo. */
int maganhangzo(char c)
{
    return c=='a' || c=='e' || c=='i' || c=='o' || c=='u';
}

int main()
{
    char c;

    while (scanf("%c", &c)==1)
        if (maganhangzo(c))
            printf("%cv%c", c, c);
        else
            printf("%c", c);

    return 0;
}

Egyszerű! A fenti, magánhangzó vizsgálatát végző függvénynek ne a beolvasott karaktert adjuk, hanem annak kisbetűsített párját. Így az nem is fogja látni, hogy nagybetűről vagy kisbetűről van szó. Innen adódik lent a maganhangzo(kisbetu(c)) kifejezés. Másrészt, a kiírásnál a v betű utáni duplázott magánhangzót ne az eredeti formájában írjuk ki, hanem kisbetűsítve. Ebből jön a printf() paramétereiben hívott kisbetu() függvény:

while (scanf("%c", &c)==1)
    if (maganhangzo(kisbetu(c)))
        printf("%cv%c", c, kisbetu(c));
    else
        printf("%c", c);

Mivel a kiírás balról jobbra halad, ezért először a legnagyobb helyiértékű számjegyre van szükségünk. Például ha 10-es számrendszerben szeretnénk kiírni a 123-at, akkor először az 1-est, utána a 2-est, végül pedig a 3-ast kell.

Ezért kell egy ciklus, amely a legnagyobb helyiértéktől a legkisebbig halad. A 123 példájában n=2-től (százasok) n=0-ig (egyesek). A megoldásban ez szerepel a kiir() függvényben. Hogy ez működni tudjon, két másik alproblémára kell még megoldás:

• Tudnunk kell, melyik a legnagyobb helyiérték. Ehhez majd megírjuk a szamjegyek_szama() függvényt.
• Ki kell tudnunk vágni a számból egy adott helyiértékű számjegyet. Ehhez pedig az n_edik_szamjegy() függvény lesz használható.

Ehhez az egyszerű feladathoz természetesen nem lenne feltétlenül szükséges függvényeket használni. De jól mutatják azt, hogyan lehet kisebb részekre bontani a problémát.

#include <stdio.h>

/* megmondja, hogy egy adott szam egy adott szamrendszerben
 * hany szamjegybol all. */
int szamjegyek_szama(int szam, int szamrendszer)
{
   int szamjegyek=0;
   while (szam>0) {
      szam/=szamrendszer;
      szamjegyek+=1;
   }

   return szamjegyek;
}

/* adott szam adott szamrendszerbeli alakjanak n. szamjegyet
 * adja vissza. n a kitevonek megfelelo hatvanykitevo,
 * vagyis n=0 adja az egyeseket, n=1 a tizeseket stb.,
 * ha epp 10-es szamrendszerben vagyunk. */
int n_edik_szamjegy(int szam, int szamrendszer, int n)
{
   /* pelda: szam=1234, n=2 -> szam=12 lesz, mert 2x osztja */
   while (n>0) {
      szam/=szamrendszer;
      n-=1;
   }
   /* pelda: szam=12 itt, szam%10 -> 2-vel ter vissza */
   return szam%szamrendszer;
}

/* adott szám kiírása adott számrendszerben. */
/* először ki kell találni, az egész hány számjegyből áll;
   mivel a legnagyobb helyiértékűt kell kiírni először. */
void kiir(int mit, int miben)
{
   int n;

   /* a kiírandó számjegyek, visszafelé */
   for (n=szamjegyek_szama(mit, miben)-1; n>=0; n-=1)
      printf("%d", n_edik_szamjegy(mit, miben, n));
}

int main()
{
   kiir(123, 10); printf("\n");
   kiir(255, 2); printf("\n");

   return 0;
}

A programban a megfelelő helyen nem véletlenül szerepel while és for ciklus. Az elsőnél a while praktikusabb (az igazi „amíg” jellegű), a másodiknál inkább a for (számlálásos jellegű).

Ehhez csak a kiírást kell módosítani, hiszen az n_edik_szamjegy() függvény már eddigi formájában is elő tudja állítani a 10-nél nagyobb számjegyeket is. A kiírandó karaktert így tudjuk előállítani:

/* Visszatér egy karakterrel, amely az adott számjegyet ábrázolja.
 * 0..9 számjegyek -> '0'..'9' karakterek.
 * 10-nél nagyobb számjegyek -> betűk 'A'-tól kezdődően. */
char szamjegy_karakter(int szj)
{
    if (szj<10)
        return szj+'0';
    else
        return szj-10+'A';
}

#include <stdio.h>

/* Visszaadja a két egész szám közül a kisebbiket. */
int min(int a, int b)
{
    if (a<b)        /* ha "a" kisebb */
        return a;
    else            /* amugy "b" kisebb, vagy egyenloek */
        return b;
}

/* Visszaadja a két egész szám közül a nagyobbikat. */
int max(int a, int b)
{
    if (a>b)
        return a;
    else
        return b;
}

/* Visszaadja a számot, ha az nagyobb, mint min, amúgy pedig min-t. */
int alulrol(int szam, int min)
{
    return max(szam, min);
}

/* Visszaadja a számot, ha az kisebb, mint max; amúgy a
 * maxot. Ugyanaz a helyzet, mint az előbbinél. */
int felulrol(int szam, int max)
{
    return min(szam, max);
}

/* A [min;max] intervallumba szorítja a megadott számot, és
 * azzal tér vissza. Csak akkor működik helyesen, ha min<=max. */
int korlatoz(int szam, int min, int max)
{
    return felulrol(alulrol(szam, min), max);
}

int main()
{
    int i;

    printf("min(5, 7)=%d\n", min(5, 7));
    printf("max(5, 7)=%d\n", max(5, 7));
    printf("alulrol(5, 0)=%d\n", alulrol(5, 0));
    printf("alulrol(-1, 0)=%d\n", alulrol(-1, 0));
    printf("felulrol(5, 0)=%d\n", felulrol(5, 0));
    printf("felulrol(-1, 0)=%d\n", felulrol(-1, 0));
    printf("-5..10 számok [0;5] közé korlátozva:\n");
    for (i=-5; i<=10; i+=1)
        printf("%d ", korlatoz(i, 0, 5));
    printf("\n");

    return 0;
}

Beugrató: az alulrol() függvény a max() hívásával oldható meg. Ugyanis ha a limit alá csúszik a szám, akkor a limit lesz a nagyobb; Ha a limit felett van, akkor pedig a szám! Ugyanígy, a felulrol() függvényben a min()-t kell használni.

Természetesen megoldhatóak lennének az utóbbiak a min() és max() használata nélkül is. A korlatoz() pedig megoldható lenne a min() és max() használatával – ebben az esetben azonban figyelni kellene arra, hogy a formális paramétereit nem szabadna min-nek és max-nak elnevezni, hiszen akkor nem lehetne belőle meghívni a min() és max() függvényeket:

int korlatoz(int szam, int min, int max) // HIBÁS!
{
    return min(max(szam, min), max);     // HIBÁS!
}

A formális paraméter neve elfedi a függvényen kívül megadott másik függvény nevét. Érdemes ezt átgondolni a fent helyesen megírt alulrol() és felulrol() esetén is! Ott is megtörténik ez, csak nem probléma, mert mindkettőnél pont a másik függvényre van szükség.

#include <stdio.h>
#include <ctype.h>

/* Visszaadja a számjegy értékét:
 * - 0-9 -> 0-9
 * - A-Z (a-z) -> 10-35
 * - egyéb karakter (érvénytelen) -> -1 */
int ertek(char c)
{
    if (isdigit(c))
        return c-'0';
    if (isalpha(c))
        return toupper(c)-'A'+10;
    /* nem szám, nem betű - ez bizony hiba */
    return -1;
}

/* beolvas egy egész számot a billentyűzetről,
 * az adott számrendszerben. visszatérési értéke
 * a beolvasott szám, vagy hiba esetén -1. */
int beolvas(int alap)
{
    int szam;
    char c;

    szam=0;
    while (scanf("%c", &c)==1 && !isspace(c)) {
        int ert = ertek(c);
        if (ert<0 || ert>=alap) /* ha hiba, vagy túl nagy az alaphoz */
            return -1;
        szam = szam*alap + ert;
    }
    return szam;
}

int main()
{
    printf("Irj 2-esben: ");
    printf("Erteke 10-esben: %d\n", beolvas(2));
    printf("Irj 16-osban: ");
    printf("Erteke 10-esben: %d\n", beolvas(16));

    return 0;
}

Induljunk ki a definícióból: tökéletes szám az, amelyik megegyezik a nála kisebb osztóinak összegével. A kisebb osztókat összeadő függvényt majd megcsináljuk később.

/* igazzal tér vissza, ha tökéletes szám */
int tokeletes(int szam)
{
    return szam==kisebboszto_osszeg(szam);
}

Barátságos számpár pedig az, amelyeknél egymásra vetítve működik ez ugyanígy.

/* igazzal tér vissza, ha barátságosak */
int baratsagos(int szam1, int szam2)
{
    return szam1==kisebboszto_osszeg(szam2) && szam2==kisebboszto_osszeg(szam1);
}

A tökéletes szám és a barátságos számok definíciója nagyon hasonlít egymáshoz. Tulajdonképpen a tökéletes szám önmaga barátja. Vegyük észre: az osztós függvény létezését feltételezve egy-egy sorban meg tudtuk oldani a problémákat! Sőt, mivel mindkét függvény ugyanannak a segédfüggvénynek a létezését feltételezi, elég azt már egyszer megírnunk! A teljes program:

#include <stdio.h>

/* visszatér a paraméterként kapott szám
   osztóinak összegével (magát a számot kivéve) */
int kisebboszto_osszeg(int szam)
{
    int osszeg, oszto;

    osszeg=0;
    for (oszto=1; oszto<=szam/2; oszto+=1)
        if (szam%oszto == 0)
            osszeg += oszto;

    return osszeg;
}

/* igazzal tér vissza, ha tökéletes szám */
int tokeletes(int szam)
{
    return szam==kisebboszto_osszeg(szam);
}

/* igazzal tér vissza, ha barátságosak */
int baratsagos(int szam1, int szam2)
{
    return szam1==kisebboszto_osszeg(szam2)
           && szam2==kisebboszto_osszeg(szam1);
}

int main()
{
    printf("6 tökéletes: %d\n", tokeletes(6));
    printf("7 tökéletes: %d\n", tokeletes(7));
    printf("220,284 barátságos: %d\n", baratsagos(220, 284));
    printf("220,285 barátságos: %d\n", baratsagos(220, 285));

    return 0;
}