1 A Mandelbrot-halmaz
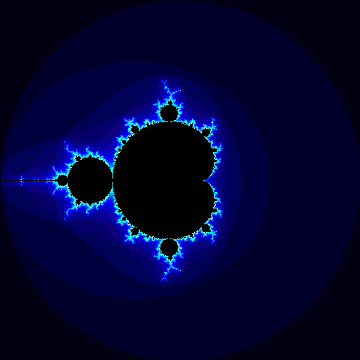
Többé-kevésbé pontosan idézve a Wikipediáról: a Mandelbrot-halmaz azon komplex számokból áll, amelyekre a következő, rekurzívan definiált sorozat nem tart a végtelenbe:
zn+1=zn2+c
Ezt a halmazt a kétdimenziós komplex számsíkon szokták ábrázolni; a képletben c az adott pont koordinátája. A dolog érdekessége, hogy a keletkező ábra részletessége végtelen nagy. Bármekkora nagyítással találhatók benne olyan részek, amelyek hasonlítanak a teljes halmaz formájára. Vagyis bármeddig nagyíthatjuk, soha nem érjük el a maximális nagyítást.
Írjunk programot, amely kirajzolja ezt a halmazt! A fenti, komplex számokon végzett műveleteket ehhez le kell írnunk valós számokkal. Felbontva valós és képzetes részre a számot: z=zr+jzi, a következő egyenletrendezés adódik. Az utolsó sorban külön látható az új z érték valós és képzetes része.
zúj=(zr+jzi)2+cr+jci
zúj=zr2+2jzrzi+j2zi2+cr+jci
zúj=zr2-zi2+cr + j(2zrzi+ci)
Mit jelent az, hogy nem tart végtelenbe a sorozat? Ez programozásilag nem igazán megfogható
fogalom, ugyanis nem tehetjük meg, hogy egy végtelenségig futó ciklust írunk ennek tesztelésére.
A számítást ezért úgy kell végezni, hogy ellenőrizzük, z értékének abszolút értéke kisebb-
e kettőnél (ha nagyobb, akkor a négyzetre emelés miatt úgyis biztosan egyre nagyobb lesz, hiszen
a szorzás egy nagyításnak felel meg); illetve számoljuk, hogy a sorozat hányadik értékét
határoztuk meg. Egy adott iterációszám felett a ciklust megszakítjuk. A |z|<2
egyenlőtlenség valós számokkal sqrt(zr*zr+zi*zi)<2-nek felel meg; mivel a
négyzetgyök szigorúan monoton függvény, ezt érdemes a kódban zr*zr+zi*zi<4-re
átírni, mert a gyökvonást meg lehet ezáltal spórolni. A számítás így néz ki:
for (y=0; y<MERETY; y++) {
for (x=0; x<MERETX; x++) {
/* a konstanst a koordinata hatarozza meg */
double cr=(x-MERETX/2)/(double)MERETX*4;
double ci=(y-MERETY/2)/(double)MERETY*4;
double zr=0, zi=0;
/* addig, amig |z|<2, vagy tul sok iteracio nem volt */
i=0;
while (i<128 && zr*zr+zi*zi<4) {
/* ez itt a z=z^2+c */
double uzr=zr*zr-zi*zi+cr;
double uzi=2*zr*zi+ci; /* http://napirajz.hu/files/zsak.jpg */
zr=uzr;
zi=uzi;
i++;
}
/* az iteraciok szama hatarozza meg a keppont szinet: i */
}
}
A fenti, színes ábrák úgy alakulnak ki, hogy az iterációk számához, azaz az i
értékéhez rendelünk színeket. Az egymás utáni színeket érdemes úgy beállítani, hogy átmenet
legyen közöttük. Ezt csinálják a letölthető kódban a szinek() és a
gradient() függvények. A színeket egy táblázatból olvassuk ki. A szinek() függvény
ezt a táblázatot alkotja meg – a megadott vörös, zöld, kék (0…255) komponensek között egyenes
átmenetet képezve.
A program: advent2-mandelbrot.c.
2 Nagyítás
Mindez persze nem túl izgalmas addig, amíg nem tudjuk nagyítani a képet, és nem tudunk navigálni rajta. Ezért a program második változatába bekerültek ezek a lehetőségek. A programba bekerült az x/y irányú eltolás, és a nagyítás értékét tároló változó:
double ex = 0, ey = 0, n = screen->w/4.0; /* eltolas es nagyitas */
Ezek értékét pedig a kurzorbillentyűk, továbbá a Q és A billentyűk hatására úgy változtatjuk, hogy a kép mozogjon, továbbá a nagyítást a kép középpontjához képest végezzük:
if (keystate[SDLK_UP]) { ey -= 2; rajzol = 1; }
if (keystate[SDLK_DOWN]) { ey += 2; rajzol = 1; }
if (keystate[SDLK_RIGHT]) { ex += 2; rajzol = 1; }
if (keystate[SDLK_LEFT]) { ex -= 2; rajzol = 1; }
if (keystate[SDLK_q]) { n *= 1.01; ex *= 1.01; ey *= 1.01; rajzol = 1; }
if (keystate[SDLK_a]) { n /= 1.01; ex /= 1.01; ey /= 1.01; rajzol = 1; }

… és már jók is vagyunk. Csak a program kicsit lassúcska néha, ha olyan területek felé navigálunk, ahol túl nagy iterációszámra van szükség. De nem gond – meg kell izzasztani a gépet! A mai processzorok kettő vagy négy magosak is lehetnek, ami azt jelenti, hogy a számításokat szétoszthatjuk a magok között. Mivel az egyes képpontokhoz tartozó számítások egymástól függetlenek, ez könnyen megy: egyik képpontot (vagy egyik sor képpontjait) számolhatja az egyik mag, a másikét pedig a másik.
Az ilyen jellegű párhuzamosításhoz legjobban az OpenMP használható. Ha a fordítónk ezt
támogatja, akkor ezzel megoldható, hogy egy kiválasztott ciklus egyes iterációit szétosszuk a
rendelkezésre álló processzormagok között. Aki több processzorral vagy processzormaggal
rendelkező gépen próbálja ki a programot (pl. egy Core2Duo-s gépen), így sokkal gyorsabb
animációt kaphat. Az alábbi direktívát írva a for() ciklus elé azt mondjuk
az OpenMP-nek, hogy ennek a ciklusnak az iterációit nyolcasával ossza szét a magok között:
#pragma omp parallel for schedule(dynamic, 8) for (y=0; y<MERETY; y++) …
Párhuzamosításkor figyelni kell arra, hogy a program több szálon fut. A szálak memóriája,
vagyis a változók viszont közösek. Ez olyan, mintha egyszerre két program férne hozzá a
változókhoz, vagyis akár felül is írhatják egymás értékeit. Mivel az egyes sorok oszlop szerinti
ciklusai eltérő helyen tarthatnak, ez azt jelenti, hogy az egyes szálak különböző x
változókkal kell rendelkezzenek. A cikluson kívül deklarált változók az OpenMP használatakor úgy
viselkednek, mintha globális változók lennének. Ha így használjuk az x változót,
helytelen eredményt kapunk. Viszont ha a cikluson belül deklaráljuk azokat a változókat,
amelyekből független példányoknak kell lenniük (jelen esetben az x-et és az
i-t), akkor a szálokon belül lokálissá válnak:
#pragma omp parallel for schedule(dynamic, 8)
for (y=0; y<MERETY; y++) {
int x; // minden szálnak saját
for (x=0; x<MERETX; x++) …
A letölthető program: advent2-zoomer.c.
Az OpenMP engedélyezéséhez a GCC fordítónál az -fopenmp paraméterre van
szükség (Code::Blocks: Project, Build Options, balra fent: project neve, Compiler
settings, Other options: -fopenmp), továbbá érdemes az optimalizálást
is engedélyezni: Compiler settings, Compiler flags, Optimize fully (for speed): -O3,
mert ettől is legalább duplájára gyorsul.
A Julia-halmaz a fentihez nagyon hasonló. A különbség annyi, hogy a c szám a számításban konstans, nem a koordináta határozza meg; helyette z kezdeti értéke függ a koordinátától. Azokra a pontokra, amelyekre c a Mandelbrot-halmazon belüli szám, a Julia-halmaz látványos formát ölt. Lásd a forráskódot!
